Question

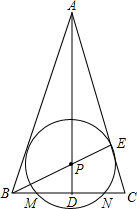已知△ABC，AB=AC，∠BAC=30°，AD⊥BC于D，E在AC上，BE=BC，BC=2

3

，半径为

2

的⊙P从B点沿BE向E点运动，
（1）当P点运动到AD与BE的交点时，求证：AB为⊙P的切线；
（2）在（1）的条件下，设⊙P与BC交于M、N两点，求MN的长．

Answer 1

考点：切线的判定

专题：证明题

分析：（1）作PF⊥AB于F，如图，根据等腰三角形的性质得∠BAD=∠CAD=

1

2

∠BAC=15°，BD=CD=

1

2

BC=

3

，利用互余得∠C=75°，而BC=BE，所以∠BEC=∠C=75°，根据三角形外角性质可计算出∠ABE=45°，则可判断△FBP为等腰直角三角形，所以PF=

2

2

BP；再根据三角形外角性质可计算出∠BPD=15°+45°=60°，在Rt△PDB中，根据含30度的直角三角形三边的关系得PD=

3

3

BD=1，PB=2PD=2，则PF=

2

，加上⊙P的半径为

2

，于是根据切线的判定方得到AB为⊙P的切线；
（2）设MD=a，根据垂径定理由PD⊥MN待定MD=ND=a，则BM=BD-MD=

3

-a，BN=MD+DN=

3

+a，再由△FBP为等腰直角三角形得BF=PF=

2

，然后根据切割线定理得到（

2

）²=（

3

-a）（

3

+a），解得a=1，再利用MN=MD+ND进行计算．

解答：（1）证明：作PF⊥AB于F，如图，
∵AB=AC，AD⊥BC，
∴∠BAD=∠CAD=

1

2

∠BAC=

1

2

×30°=15°，BD=CD=

1

2

BC=

3

，
∴∠C=90°-∠CAD=75°，
而BC=BE，
∴∠BEC=∠C=75°，
∵∠BEC=∠BAE+∠ABE，
∴∠ABE=75°-30°=45°，
∴△FBP为等腰直角三角形，
∴PF=

2

2

BP；
∵∠BPD=∠BAP+∠ABP，
∴∠BPD=15°+45°=60°，
在Rt△PDB中，PD=

3

3

BD=1，
∴PB=2PD=2，
∴PF=

2

2

×2=

2

，
∵⊙P的半径为

2

，
∴⊙P的半径PF垂直AB，
∴AB为⊙P的切线；
（2）解：设MD=a，
∵PD⊥MN，
∴MD=ND=a，
∴BM=BD-MD=

3

-a，BN=MD+DN=

3

+a，
∵△FBP为等腰直角三角形，
∴BF=PF=

2

，
∵BF为⊙P的切线，
∴BF²=BM•BN，即（

2

）²=（

3

-a）（

3

+a），解得a=1，
∴MN=MD+ND=1+1=2．

点评：本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了垂径定理切割线定理和等腰三角形的性质．