Question

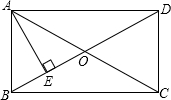如图，在矩形ABCD中，AE⊥BD于E，且BE：ED=1：3，求证：AC=2AB．

Answer 1

考点：矩形的性质

专题：证明题

分析：根据矩形的对角线互相平分且相等可得OA=OB=OC=OD，再求出BE=OE，从而判断出AE垂直平分BO，根据线段垂直平分线上的点到两端点的距离相等可得AB=OA，然后根据AC=OA+OC等量代换即可得证．

解答：证明：在矩形ABCD中，OA=OB=OC=OD，
∵BE：ED=1：3，
∴BE=OE，
∵AE⊥BD，
∴AE垂直平分BO，
∴AB=OA，
∵AC=OA+OC，
∴AC=2AB．

点评：本题考查了矩形的性质，线段垂直平分线上的点到两端点的距离相等的性质，熟记矩形的对角线互相平分且相等是解题的关键．