题目内容
14.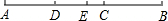 如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )
如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )| A. | 8cm | B. | 12cm | C. | 14cm | D. | 10cm |
分析 根据比值,可得 AC、BC,根据线段中点的性质,可得AD,AE,根据线段的和差,可得关于x的方程,根据解方程,可得x的值,可得答案.
解答 解:由AC:CB=3:2,得
AC=3x,BC=2x.
AB=AC+BC=5x.
由D、E两点分别为AC、AB的中点,得
AD=$\frac{1}{2}$AC=$\frac{3}{2}$x,AE=$\frac{1}{2}$AB=$\frac{5}{2}$x.
由线段的和差,得
DE=AE-AD=$\frac{5}{2}$x-$\frac{3}{2}$x=x.
DE=2,
x=2,
AB=5x=10cm,
故选:D.
点评 本题考查了两点间的距离,利用比值得出AC=3x,BC=2x是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.小明和3个女生、4个男生玩丢手绢的游戏,如果小明随意将手绢丢在一名同学后面,那么这名同学不是女生的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{4}{7}$ | D. | $\frac{3}{7}$ |
3.下列运算正确的是( )
| A. | b•b3=b4 | B. | x3+x3=x6 | C. | 4a3•2a2=8a6 | D. | 5a2-3a2=2 |
4.下列几组数据中,能作为直角三角形三边长的是( )
| A. | 2,3,4 | B. | 1,2,3 | C. | 1,$\frac{1}{2}$,$\frac{1}{3}$ | D. | 7,24,25 |
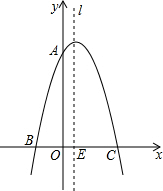 已知二次函数y=-x2+bx+c的图象与x轴交于B(-2,0),C(4,0)两点,点E是对称轴l与x轴的交点.
已知二次函数y=-x2+bx+c的图象与x轴交于B(-2,0),C(4,0)两点,点E是对称轴l与x轴的交点. 如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知E′D′=2,则BC的值是( )
如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知E′D′=2,则BC的值是( )