题目内容
1.(1)解方程:$\frac{x}{x-1}$-$\frac{2x-1}{{x}^{2}-1}$=1(2)化简$\frac{1}{a+1}$-$\frac{a+3}{{{a^2}-1}}$×$\frac{{a}^{2}-2a+1}{{a}^{2}+4a+3}$,并用选择一个你喜欢的数代入求值.
分析 (1)利用解分式方程的步骤与方法得出答案即可;
(2)先算乘法因式分解约分化简,再算通分加法,选择合适的数值代入求得答案即可.
解答 解:(1)$\frac{x}{x-1}$-$\frac{2x-1}{{x}^{2}-1}$=1
方程两边同乘(x+1)(x-1)得
x(x+1)-(2x-1)=(x+1)(x-1)
解得:x=2
检验:当x=2时,(x+1)(x-1)≠0,
所以x=2是原分式方程的解;
(2)原式=$\frac{1}{a+1}$-$\frac{a+3}{(a+1)(a-1)}$×$\frac{(a-1)^{2}}{(a+1)(a+3)}$
=$\frac{1}{a+1}$-$\frac{a-1}{(a+1)^{2}}$
=$\frac{2}{(a+1)^{2}}$
当x=2时,原式=$\frac{2}{9}$.
点评 此题考查解分式方程,分式的化简求值,掌握解答的步骤与方法是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列去括号不正确的是( )
| A. | (a+$\frac{1}{2}$b)-(-$\frac{1}{3}$c+$\frac{2}{7}$)=a+$\frac{1}{2}$b+$\frac{1}{3}c$-$\frac{2}{7}$ | B. | m+(-n+a-b)=m-n+a-b | ||
| C. | x-(3y-$\frac{1}{2}$)=x-3y+$\frac{1}{2}$ | D. | -$\frac{1}{2}$(4x-6y+3)=-2x+3y+3 |
 如图,在△ABC中,点D是BC的中点,FD⊥ED,延长ED到点P.使ED=PD,连结FP与CP,试判断BE+CF与EF的大小关系.
如图,在△ABC中,点D是BC的中点,FD⊥ED,延长ED到点P.使ED=PD,连结FP与CP,试判断BE+CF与EF的大小关系.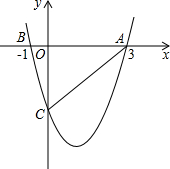 如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.
如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.