题目内容
8. 如图,已知DE为△ABC中∠BAC的外角平分线,BD、CE均为DE的垂线,求证:AF∥EC.
如图,已知DE为△ABC中∠BAC的外角平分线,BD、CE均为DE的垂线,求证:AF∥EC.
分析 由已知条件和对顶角相等得出∠2=∠3,由已知条件得出∠ADB=∠AEC=90°,BD∥CE,得出△BDA∽CEA,△BDF∽△ECF,得出对应边成比例AD:AE=BD:CE,BD:CE=DF:FC,因此AD:AE=DF:FC,即可得出AF∥EC.
解答 证明:如图所示: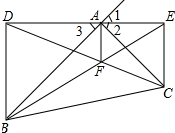
∵∠1=∠2,∠1=∠3,
∴∠2=∠3,
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,BD∥CE,
∴△BDA∽△CEA,△BDF∽△ECF,
∴AD:AE=BD:CE,BD:CE=DF:FC,
∴AD:AE=DF:FC,
∴AF∥EC.
点评 本题考查了相似三角形的判定与性质、平行线的判定与性质;熟练掌握相似三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
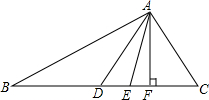 如图,AD、AE、AF分别是△ABC的中线、角平分线和高,请你指出图中相等的角及相等的线段.
如图,AD、AE、AF分别是△ABC的中线、角平分线和高,请你指出图中相等的角及相等的线段.