题目内容
11.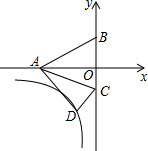 如图,在平面直角坐标系中有一个Rt△ABO,点A的坐标为(-2,0),点B的坐标为(0,1),将△ABO绕点A按顺时针方向旋转45°,点O的对应点D恰好落在双曲线y=$\frac{k}{x}$(x<0)上,在此双曲线上存在一点E,若点E到x轴的距离为2,则点E的坐标为( )
如图,在平面直角坐标系中有一个Rt△ABO,点A的坐标为(-2,0),点B的坐标为(0,1),将△ABO绕点A按顺时针方向旋转45°,点O的对应点D恰好落在双曲线y=$\frac{k}{x}$(x<0)上,在此双曲线上存在一点E,若点E到x轴的距离为2,则点E的坐标为( )| A. | (-2,1-$\sqrt{2}$) | B. | (-2,$\sqrt{2}-1$) | C. | (1-$\sqrt{2}$,-2) | D. | ($\sqrt{2}-1,-2$) |
分析 作DH⊥OA于H,如图,根据旋转的性质得AD=AO=2,∠OAD=45°,则可判断△ADH为等腰直角三角形,则DH=AH=$\frac{\sqrt{2}}{2}$AD=$\sqrt{2}$,易得D(-2+$\sqrt{2}$,-$\sqrt{2}$),利用待定系数法可确定反比例函数的解析式,然后计算函数值为-2所对应的自变量的值即可得到E点坐标.
解答 解:作DH⊥OA于H,如图,
∵△ABO绕点A按顺时针方向旋转45°,
∴AD=AO=2,∠OAD=45°,
∴△ADH为等腰直角三角形,
∴DH=AH=$\frac{\sqrt{2}}{2}$AD=$\sqrt{2}$,
∴OH=OA-AH=2-$\sqrt{2}$,
∴D(-2+$\sqrt{2}$,-$\sqrt{2}$),
把D(-2+$\sqrt{2}$,-$\sqrt{2}$)代入y=$\frac{k}{x}$得k=(-2+$\sqrt{2}$)×(-$\sqrt{2}$)=2$\sqrt{2}$-2,
∴反比例函数解析式为y=$\frac{2\sqrt{2}-2}{x}$(x<0),
当y=-2时,$\frac{2\sqrt{2}-2}{x}$=-2,解得x=1-$\sqrt{2}$,
∴E点坐标为(1-$\sqrt{2}$,-2).
故选C.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.也考查了反比例函数图象上点的坐标特征.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
2.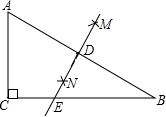 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )| A. | 2 | B. | $\frac{10}{3}$ | C. | $\frac{15}{8}$ | D. | $\frac{15}{2}$ |
19.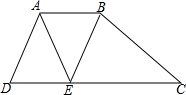 如图,在四边形ABCD中,AB∥CD,AB=4,CD=11,点E在边CD上,AD∥BE,若AD=AB,且cos∠BEC=$\frac{1}{2}$,则四边形ABCE的面积为( )
如图,在四边形ABCD中,AB∥CD,AB=4,CD=11,点E在边CD上,AD∥BE,若AD=AB,且cos∠BEC=$\frac{1}{2}$,则四边形ABCE的面积为( )
 如图,在四边形ABCD中,AB∥CD,AB=4,CD=11,点E在边CD上,AD∥BE,若AD=AB,且cos∠BEC=$\frac{1}{2}$,则四边形ABCE的面积为( )
如图,在四边形ABCD中,AB∥CD,AB=4,CD=11,点E在边CD上,AD∥BE,若AD=AB,且cos∠BEC=$\frac{1}{2}$,则四边形ABCE的面积为( )| A. | $\sqrt{3}$ | B. | 11$\sqrt{3}$ | C. | 15$\sqrt{3}$ | D. | 22$\sqrt{3}$ |
6.计算(200-2)(200+2)的结果是( )
| A. | 39998 | B. | 39996 | C. | 29996 | D. | 39992 |
3.若一元二次方程x2+2x+m+1=0有实数根,则( )
| A. | m的最小值是1 | B. | m的最小值是-1 | C. | m的最大值是0 | D. | m的最大值是2 |
20.点A(-1,2)与A′关于x轴对称,则点A′的坐标是( )
| A. | (1,2) | B. | (1,-2) | C. | (-1,-2) | D. | (-1,2) |
1. 为了解某校中学生获取资讯的主要渠道,该校随机抽取若干名学生进行调查,根据调查结果绘制条形统计图如图所示,其中A为电视、B为网格、C为报纸、D为身边的人、E为其他,茗茗想将图中用扇形统计图,则B所对应扇形圆心角的度数为( )
为了解某校中学生获取资讯的主要渠道,该校随机抽取若干名学生进行调查,根据调查结果绘制条形统计图如图所示,其中A为电视、B为网格、C为报纸、D为身边的人、E为其他,茗茗想将图中用扇形统计图,则B所对应扇形圆心角的度数为( )
 为了解某校中学生获取资讯的主要渠道,该校随机抽取若干名学生进行调查,根据调查结果绘制条形统计图如图所示,其中A为电视、B为网格、C为报纸、D为身边的人、E为其他,茗茗想将图中用扇形统计图,则B所对应扇形圆心角的度数为( )
为了解某校中学生获取资讯的主要渠道,该校随机抽取若干名学生进行调查,根据调查结果绘制条形统计图如图所示,其中A为电视、B为网格、C为报纸、D为身边的人、E为其他,茗茗想将图中用扇形统计图,则B所对应扇形圆心角的度数为( )| A. | 130° | B. | 129.6° | C. | 128.6° | D. | 119.6° |
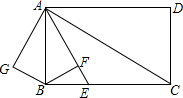 如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.
如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.