题目内容
20．点A（-1，2）与A′关于x轴对称，则点A′的坐标是（ ）| A． | （1，2） | B． | （1，-2） | C． | （-1，-2） | D． | （-1，2） |
分析 结合关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数．即点P（x，y）关于x轴的对称点P′的坐标是（x，-y），进而得出答案．
解答 解：∵点A（-1，2）与A′关于x轴对称，
∴点A′的坐标是：（-1，-2）．
故选：C．
点评 此题主要考查了关于x轴对称点的性质，正确把握横纵坐标的关系是解题关键．
练习册系列答案
相关题目
10．我们规定，对于任意实数m，符号[m]表示小于或等于m的最大整数，例如：[2，1]=2，[2]=2，[-2，1]=-3，若对于整数x有[$\frac{3x-1}{2}$]=-5，则符合题意的x有（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 无数个 |
11．
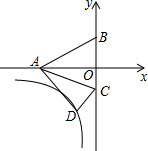如图，在平面直角坐标系中有一个Rt△ABO，点A的坐标为（-2，0），点B的坐标为（0，1），将△ABO绕点A按顺时针方向旋转45°，点O的对应点D恰好落在双曲线y=$\frac{k}{x}$（x＜0）上，在此双曲线上存在一点E，若点E到x轴的距离为2，则点E的坐标为（ ）
如图，在平面直角坐标系中有一个Rt△ABO，点A的坐标为（-2，0），点B的坐标为（0，1），将△ABO绕点A按顺时针方向旋转45°，点O的对应点D恰好落在双曲线y=$\frac{k}{x}$（x＜0）上，在此双曲线上存在一点E，若点E到x轴的距离为2，则点E的坐标为（ ）| A． | （-2，1-$\sqrt{2}$） | B． | （-2，$\sqrt{2}-1$） | C． | （1-$\sqrt{2}$，-2） | D． | （$\sqrt{2}-1，-2$） |
5．
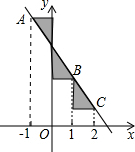如图，点A、B、C在一次函数y=-2x+m的图象上，它们的横坐标依次为-1，1，2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积之和是（ ）
如图，点A、B、C在一次函数y=-2x+m的图象上，它们的横坐标依次为-1，1，2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积之和是（ ）| A． | 3（m-1） | B． | $\frac{3}{2}（m-2）$ | C． | 1 | D． | 3 |
两位同学玩“石头、剪子、布”游戏，随机出手一次，两人手势相同的概率是$\frac{1}{3}$．
9．
某企业为一商场提供家电配件，从去年1至9月，该配件的原材料价格一路攀升，每件配件的原材料价格y1（元）与月份x（1≤x≤9，且x取整数）之间的函数关系如下表：
随着国家调控措施的出台，原材料价格的涨势趋缓，10至12月每件配件的原材料价格y2（元）与月份x（10≤x≤12，且x取整数）之间存在如图所示的变化趋势：
（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y1与x之间的函数关系式，根据如图所示的变化趋势，直接写出y2与x之间满足的一次函数关系式；
（2）若去年该配件每件的售价为100元，生产每件配件的人力成本为5元，其它成本3元，该配件在1至9月的销售量p1（万件）与月份x满足函数关系式p1=0.1x+1.1（1≤x≤9，且x取整数），10至12月的销售量p2（万件）与月份x满足函数关系式p2=-0.1x+2.9（10≤x≤12，且x取整数）．求去年哪个月销售该配件的利润最大，并求出这个最大利润；
（3）今年1月份，每件配件的原材料价格均比去年10月上涨8元，人力成本比去年增加1元，其它成本没有变化，该企业将每件配件的售价在去年的基础上提高a%，与此同时每月销售量均在去年12月的基础上减少8a%．这样，该月完成了17万元利润的任务，请你计算出a的值．
某企业为一商场提供家电配件，从去年1至9月，该配件的原材料价格一路攀升，每件配件的原材料价格y1（元）与月份x（1≤x≤9，且x取整数）之间的函数关系如下表：| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1（元/件） | 56 | 58 | 60 | 62 | 64 | 66 | 68 | 70 | 72 |
（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y1与x之间的函数关系式，根据如图所示的变化趋势，直接写出y2与x之间满足的一次函数关系式；
（2）若去年该配件每件的售价为100元，生产每件配件的人力成本为5元，其它成本3元，该配件在1至9月的销售量p1（万件）与月份x满足函数关系式p1=0.1x+1.1（1≤x≤9，且x取整数），10至12月的销售量p2（万件）与月份x满足函数关系式p2=-0.1x+2.9（10≤x≤12，且x取整数）．求去年哪个月销售该配件的利润最大，并求出这个最大利润；
（3）今年1月份，每件配件的原材料价格均比去年10月上涨8元，人力成本比去年增加1元，其它成本没有变化，该企业将每件配件的售价在去年的基础上提高a%，与此同时每月销售量均在去年12月的基础上减少8a%．这样，该月完成了17万元利润的任务，请你计算出a的值．
10．关于抛物线y=x2-（a+1）x+a-2，下列说法错误的是（ ）
| A． | 开口向上 | B． | 当a=2时，经过坐标原点O | ||
| C． | a＞0时，对称轴在y轴左侧 | D． | 不论a为何值，都经过定点（1，-2） |