题目内容
2.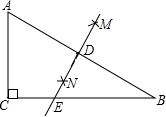 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )| A. | 2 | B. | $\frac{10}{3}$ | C. | $\frac{15}{8}$ | D. | $\frac{15}{2}$ |
分析 根据勾股定理求出BC,根据线段垂直平分线性质求出AE=BE,根据勾股定理求出AE,再根据勾股定理求出DE即可.
解答 解:在Rt△ACB中,由勾股定理得:BC=$\sqrt{{5}^{2}-{3}^{2}}$=4,
连接AE,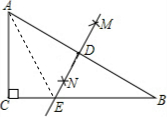
从作法可知:DE是AB的垂直平分线,
根据性质得出AE=BE,
在Rt△ACE中,由勾股定理得:AC2+CE2=AE2,
即32+(4-AE)2=AE2,
解得:AE=$\frac{25}{8}$,
在Rt△ADE中,AD=$\frac{1}{2}$AB=$\frac{5}{2}$,由勾股定理得:DE2+($\frac{5}{2}$)2=($\frac{25}{8}$)2,
解得:DE=$\frac{15}{8}$.
故选C.
点评 本题考查了线段垂直平分线性质,勾股定理的应用,能灵活运用勾股定理得出方程是解此题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
15.已知抛物线y=ax2+bx-3(a≠0)的对称轴为x=1,且经过点A(-1,0),则下列函数的图象可以由抛物线y=ax2+bx-3(a≠0)平移得到的是( )
| A. | y=x2+x-3 | B. | y=2(x-1)2-3 | C. | y=$\frac{1}{2}$(x-1)(x+1) | D. | y=3x2-3 |
10.我们规定,对于任意实数m,符号[m]表示小于或等于m的最大整数,例如:[2,1]=2,[2]=2,[-2,1]=-3,若对于整数x有[$\frac{3x-1}{2}$]=-5,则符合题意的x有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
7.7的平方根等于( )
| A. | $\sqrt{7}$ | B. | 49 | C. | ±49 | D. | ±$\sqrt{7}$ |
14. 一次函数y=kx+b(k≠0)的图象如图所示,当y<0时,x的取值范围是( )
一次函数y=kx+b(k≠0)的图象如图所示,当y<0时,x的取值范围是( )
 一次函数y=kx+b(k≠0)的图象如图所示,当y<0时,x的取值范围是( )
一次函数y=kx+b(k≠0)的图象如图所示,当y<0时,x的取值范围是( )| A. | x<0 | B. | x<3 | C. | x<4 | D. | x>4 |
11.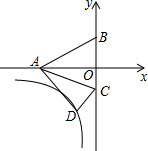 如图,在平面直角坐标系中有一个Rt△ABO,点A的坐标为(-2,0),点B的坐标为(0,1),将△ABO绕点A按顺时针方向旋转45°,点O的对应点D恰好落在双曲线y=$\frac{k}{x}$(x<0)上,在此双曲线上存在一点E,若点E到x轴的距离为2,则点E的坐标为( )
如图,在平面直角坐标系中有一个Rt△ABO,点A的坐标为(-2,0),点B的坐标为(0,1),将△ABO绕点A按顺时针方向旋转45°,点O的对应点D恰好落在双曲线y=$\frac{k}{x}$(x<0)上,在此双曲线上存在一点E,若点E到x轴的距离为2,则点E的坐标为( )
 如图,在平面直角坐标系中有一个Rt△ABO,点A的坐标为(-2,0),点B的坐标为(0,1),将△ABO绕点A按顺时针方向旋转45°,点O的对应点D恰好落在双曲线y=$\frac{k}{x}$(x<0)上,在此双曲线上存在一点E,若点E到x轴的距离为2,则点E的坐标为( )
如图,在平面直角坐标系中有一个Rt△ABO,点A的坐标为(-2,0),点B的坐标为(0,1),将△ABO绕点A按顺时针方向旋转45°,点O的对应点D恰好落在双曲线y=$\frac{k}{x}$(x<0)上,在此双曲线上存在一点E,若点E到x轴的距离为2,则点E的坐标为( )| A. | (-2,1-$\sqrt{2}$) | B. | (-2,$\sqrt{2}-1$) | C. | (1-$\sqrt{2}$,-2) | D. | ($\sqrt{2}-1,-2$) |
 如图,在直角坐标系xOy中,直线l:y=ax+b交x轴于点A(-2,0),交y轴于点B(0,2),半径为$\sqrt{2}$的⊙P与x轴相切于点C($\sqrt{2}$,0).
如图,在直角坐标系xOy中,直线l:y=ax+b交x轴于点A(-2,0),交y轴于点B(0,2),半径为$\sqrt{2}$的⊙P与x轴相切于点C($\sqrt{2}$,0). 两位同学玩“石头、剪子、布”游戏,随机出手一次,两人手势相同的概率是$\frac{1}{3}$.
两位同学玩“石头、剪子、布”游戏,随机出手一次,两人手势相同的概率是$\frac{1}{3}$.