��Ŀ����
16��2014����п�����������������ʯ��ׯ�ĺӱ�����ְѧԺ��֯������ʦ�ֱ������żҿڡ��е¡���������ˮ����̨����ɽ�߸����н�����������ѧԱ���������ǰ�����صij�Ʊ�����б���10�ţ��żҿ�17�ţ��е�13�ţ�����16�ţ���ˮ10�ţ���ɽ19�ţ���1����ȥ��̨�ij�Ʊռȫ����Ʊ��15%����ȥ��̨�ij�Ʊ�ж����ţ�
��2������ѧԺ���������ȡ�ķ�ʽ����Ʊ��С�ŵ�һ�������еij�Ʊ�������ȡһ�ţ����г�Ʊ����״����С���ʵ���ȫ��ͬ������С�ų鵽ȥ����ɽ�ij�Ʊ�ĸ����Ƕ��٣�
��3������ѧԺ�˴ι���ij�Ʊ�У�ǰ����������21.5Ԫ��ǰ���żҿڵ���64.5Ԫ��ǰ���еµ���75Ԫ��ǰ����������24.5Ԫ��ǰ����ˮ��21.5Ԫ��ǰ����ɽ����72Ԫ��ǰ����̨����16.5Ԫ�����ѧԺ�˴ι���ij�Ʊƽ��ÿ�Ŷ���Ԫ��
���� ��1����������ȥ��̨�ij�Ʊռȫ����Ʊ��15%�г����̽�ɣ�
��2�����ݸ��ʵĹ�ʽ��ɣ�
��3������ƽ��������ɣ�
��� �⣺��1����ȥ��̨�ij�Ʊ��x�ţ��������
$\frac{x}{10+17+13+16+10+19+x}$=15%��
���x=15��
��ȥ��̨�ij�Ʊ��15�ţ�
��2����ǰ�����ص���Ʊ��Ϊ100�ţ�
��ǰ����ɽ�ij�Ʊ��19�ţ�
��С�ų鵽ȥ����ɽ�ij�Ʊ�ĸ�����$\frac{19}{100}$��
��3���������$\frac{10��21.5+17��64.5+13��75+16��24.5+10��21.5+19��72+15��16.5}{100}$=45.09��
�𣺸�ѧԺ�˴ι���ij�Ʊƽ��ÿ��45.09Ԫ��
���� ���⿼��һԪһ�η��̵�Ӧ�ã��ؼ��Ǹ���ȥ��̨�ij�Ʊռȫ����Ʊ��15%�г����̣�

��ϰ��ϵ�д�
 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
�����Ŀ
7��7��ƽ�������ڣ�������
| A�� | $\sqrt{7}$ | B�� | 49 | C�� | ��49 | D�� | ��$\sqrt{7}$ |
4���ֽ���Ϊ3cm���߶�AB����ƽ��6cm�õ��߶�A��B�䣬���B���B��֮��ľ���Ϊ��������
| A�� | 0cm | B�� | 3cm | C�� | 6cm | D�� | 9cm |
11��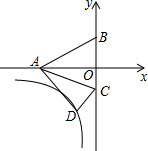 ��ͼ����ƽ��ֱ������ϵ����һ��Rt��ABO����A������Ϊ��-2��0������B������Ϊ��0��1��������ABO�Ƶ�A��˳ʱ�뷽����ת45�㣬��O�Ķ�Ӧ��Dǡ������˫����y=$\frac{k}{x}$��x��0���ϣ��ڴ�˫�����ϴ���һ��E������E��x��ľ���Ϊ2�����E������Ϊ��������
��ͼ����ƽ��ֱ������ϵ����һ��Rt��ABO����A������Ϊ��-2��0������B������Ϊ��0��1��������ABO�Ƶ�A��˳ʱ�뷽����ת45�㣬��O�Ķ�Ӧ��Dǡ������˫����y=$\frac{k}{x}$��x��0���ϣ��ڴ�˫�����ϴ���һ��E������E��x��ľ���Ϊ2�����E������Ϊ��������
 ��ͼ����ƽ��ֱ������ϵ����һ��Rt��ABO����A������Ϊ��-2��0������B������Ϊ��0��1��������ABO�Ƶ�A��˳ʱ�뷽����ת45�㣬��O�Ķ�Ӧ��Dǡ������˫����y=$\frac{k}{x}$��x��0���ϣ��ڴ�˫�����ϴ���һ��E������E��x��ľ���Ϊ2�����E������Ϊ��������
��ͼ����ƽ��ֱ������ϵ����һ��Rt��ABO����A������Ϊ��-2��0������B������Ϊ��0��1��������ABO�Ƶ�A��˳ʱ�뷽����ת45�㣬��O�Ķ�Ӧ��Dǡ������˫����y=$\frac{k}{x}$��x��0���ϣ��ڴ�˫�����ϴ���һ��E������E��x��ľ���Ϊ2�����E������Ϊ��������| A�� | ��-2��1-$\sqrt{2}$�� | B�� | ��-2��$\sqrt{2}-1$�� | C�� | ��1-$\sqrt{2}$��-2�� | D�� | ��$\sqrt{2}-1��-2$�� |
1�����м����У���ȷ���ǣ�������
| A�� | -2��a-b��=-2a-2b | B�� | $\sqrt{5}-\sqrt{2}=\sqrt{3}$ | C�� | $\frac{-x+y}{x-y}=-1$ | D�� | ��2a2b��2=2a4b2 |
5��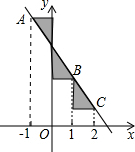 ��ͼ����A��B��C��һ�κ���y=-2x+m��ͼ���ϣ����ǵĺ���������Ϊ-1��1��2���ֱ����Щ����x����y��Ĵ��ߣ���ͼ����Ӱ���ֵ����֮���ǣ�������
��ͼ����A��B��C��һ�κ���y=-2x+m��ͼ���ϣ����ǵĺ���������Ϊ-1��1��2���ֱ����Щ����x����y��Ĵ��ߣ���ͼ����Ӱ���ֵ����֮���ǣ�������
 ��ͼ����A��B��C��һ�κ���y=-2x+m��ͼ���ϣ����ǵĺ���������Ϊ-1��1��2���ֱ����Щ����x����y��Ĵ��ߣ���ͼ����Ӱ���ֵ����֮���ǣ�������
��ͼ����A��B��C��һ�κ���y=-2x+m��ͼ���ϣ����ǵĺ���������Ϊ-1��1��2���ֱ����Щ����x����y��Ĵ��ߣ���ͼ����Ӱ���ֵ����֮���ǣ�������| A�� | 3��m-1�� | B�� | $\frac{3}{2}��m-2��$ | C�� | 1 | D�� | 3 |
6�� ������ҹ�ij����A����B��2013��5����12�µ���ƽ����Ʒס���ɽ�������λ���ף�ͳ�Ʊ���
������ҹ�ij����A����B��2013��5����12�µ���ƽ����Ʒס���ɽ�������λ���ף�ͳ�Ʊ���
��1����ͼ�е������л�������ͳ��ͼ��ʾA����B�����·�ƽ����Ʒס���ɽ����ı仯�����
��2��A��B������ƽ����Ʒס���ɽ�����������·���8�£���ƽ����Ʒס���ɽ��������С���·���9�£�
 ������ҹ�ij����A����B��2013��5����12�µ���ƽ����Ʒס���ɽ�������λ���ף�ͳ�Ʊ���
������ҹ�ij����A����B��2013��5����12�µ���ƽ����Ʒס���ɽ�������λ���ף�ͳ�Ʊ���| �·� | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A�� | 320 | 315 | 325 | 310 | 315 | 305 | 340 | 315 |
| B�� | 330 | 325 | 315 | 345 | 320 | 315 | 310 | 335 |
��2��A��B������ƽ����Ʒס���ɽ�����������·���8�£���ƽ����Ʒס���ɽ��������С���·���9�£�
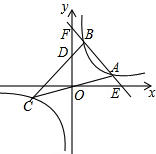 ��֪��һ�κ���y=-2x+10��ͼ���뷴��������y=$\frac{k}{x}$��k��0����ͼ���ཻ��A��B���㣨A��B���Ҳࣩ��ֱ��OA��˷���������ͼ�����һ֧������һ��C������BC��y���ڵ�D��$\frac{BC}{BD}$=$\frac{5}{2}$����ABC�����=10��
��֪��һ�κ���y=-2x+10��ͼ���뷴��������y=$\frac{k}{x}$��k��0����ͼ���ཻ��A��B���㣨A��B���Ҳࣩ��ֱ��OA��˷���������ͼ�����һ֧������һ��C������BC��y���ڵ�D��$\frac{BC}{BD}$=$\frac{5}{2}$����ABC�����=10��