题目内容
3．若一元二次方程x2+2x+m+1=0有实数根，则（ ）| A． | m的最小值是1 | B． | m的最小值是-1 | C． | m的最大值是0 | D． | m的最大值是2 |
分析 根据一元二次方程ax2+bx+c=0（a≠0）的根的判别式的意义得到△≥0，即22-4（m+1）≥0，解不等式即可．
解答 解：∵一元二次方程x2+2x+m+1=0有实数根，
∴△≥0，即22-4（m+1）≥0，
解得m≤0．
故选：C．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
相关题目
如图，在直角坐标系xOy中，直线l：y=ax+b交x轴于点A（-2，0），交y轴于点B（0，2），半径为$\sqrt{2}$的⊙P与x轴相切于点C（$\sqrt{2}$，0）．
14．
一次函数y=kx+b（k≠0）的图象如图所示，当y＜0时，x的取值范围是（ ）
一次函数y=kx+b（k≠0）的图象如图所示，当y＜0时，x的取值范围是（ ）| A． | x＜0 | B． | x＜3 | C． | x＜4 | D． | x＞4 |
11．
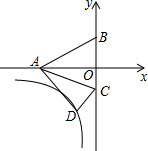如图，在平面直角坐标系中有一个Rt△ABO，点A的坐标为（-2，0），点B的坐标为（0，1），将△ABO绕点A按顺时针方向旋转45°，点O的对应点D恰好落在双曲线y=$\frac{k}{x}$（x＜0）上，在此双曲线上存在一点E，若点E到x轴的距离为2，则点E的坐标为（ ）
如图，在平面直角坐标系中有一个Rt△ABO，点A的坐标为（-2，0），点B的坐标为（0，1），将△ABO绕点A按顺时针方向旋转45°，点O的对应点D恰好落在双曲线y=$\frac{k}{x}$（x＜0）上，在此双曲线上存在一点E，若点E到x轴的距离为2，则点E的坐标为（ ）| A． | （-2，1-$\sqrt{2}$） | B． | （-2，$\sqrt{2}-1$） | C． | （1-$\sqrt{2}$，-2） | D． | （$\sqrt{2}-1，-2$） |
两位同学玩“石头、剪子、布”游戏，随机出手一次，两人手势相同的概率是$\frac{1}{3}$．