题目内容
5.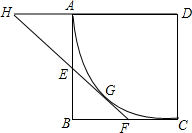 如图,正方形ABCD的边长为6,以D为圆心,DA为半径作⊙D,E在AB上,EF切⊙D于G,交BC于F.
如图,正方形ABCD的边长为6,以D为圆心,DA为半径作⊙D,E在AB上,EF切⊙D于G,交BC于F.(1)若AE=2.求证:BF=CF;
(2)若CF=2,FE的延长线交直线A于H,求DH的长.
分析 (1)利用切线长定理得到EG=EA=2,FG=FC,设FC=x,则GF=x,BF=6-x,则在Rt△BEF中,利用勾股定理得到42+(6-x)2=(2+x)2,解得x=3,于是可判断BF=CF;
(2)用同样方法就是出AE=3,再证明△AEH∽△BEF,通过相似比计算出AH=4,然后计算AH+DA即可.
解答 (1)证明:∵四边形ABCD为正方形,
∴∠BAD=∠BCD=∠B=90°,BA=BC=6,
∴BA和BC与⊙D相切,
∵EF切⊙D于G,
∴EG=EA=2,FG=FC,
设FC=x,则GF=x,BF=6-x,
在Rt△BEF中,∵BE2+BF2=EF2,
∴42+(6-x)2=(2+x)2,解得x=3,
∵BF=6-x=3,CF=3,
∴BF=CF;
(2)解:∵CF=2,
∴BF=4,
设AE=t,则EG=t,BE=6-t,
在Rt△BEF中,∵BF2+BE2=EF2,
∴42+(6-t)2=(2+t)2,解得t=3,
∴AE=3,
∵AH∥BF,
∴△AEH∽△BEF,
∴AH:BF=AE:BE,即AH:4=3:3,
∴AH=4,
∴DH=AH+DA=10.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.解决本题的关键是利用切线长定理得到EA=EG,FC=FG.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
16.“$\frac{16}{49}$的平方根是±$\frac{4}{7}$”用数学式表示为( )
| A. | $\sqrt{\frac{16}{49}}$=±$\frac{4}{7}$ | B. | $\sqrt{\frac{16}{49}}$=$\frac{4}{7}$ | C. | ±$\sqrt{\frac{16}{49}}$=±$\frac{4}{7}$ | D. | -$\sqrt{\frac{16}{49}}$=-$\frac{4}{7}$ |
10.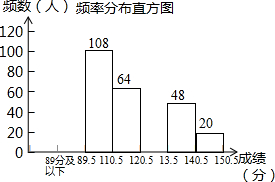 某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
频率分布表
请你根据不完整的频率分布表,解答下列问题:
(1)补全频率分布表;
(2)补全频数分布直方图;
(3)若将得分转化为等级,规定得分“89分及以下”分评为“D”,“89.5-110.5分”评为“C”,“110.5-130.5扥”评为“B”,“130.5-150.5分”评为“A”,这次15000名学生中约有多少人评为“D”?如果随机抽取一名学生的成绩等级,则这名学生的成绩评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由.
 某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:频率分布表
| 分组 | 频数 | 频率 |
| 89分及以下 | ||
| 89.5-110.5 | 108 | |
| 110.5-120.5 | 64 | 0.16 |
| 120.5-130.5 | 0.20 | |
| 130.5-140.5 | 48 | |
| 140.5-150.5 | 20 | 0.05 |
| 合计 | 400 | 1 |
(1)补全频率分布表;
(2)补全频数分布直方图;
(3)若将得分转化为等级,规定得分“89分及以下”分评为“D”,“89.5-110.5分”评为“C”,“110.5-130.5扥”评为“B”,“130.5-150.5分”评为“A”,这次15000名学生中约有多少人评为“D”?如果随机抽取一名学生的成绩等级,则这名学生的成绩评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由.
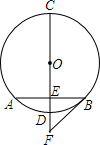 如图,CD是⊙O的直径,弦AB⊥CD于点E,且AB=2$\sqrt{2}$,DE=2-$\sqrt{2}$.
如图,CD是⊙O的直径,弦AB⊥CD于点E,且AB=2$\sqrt{2}$,DE=2-$\sqrt{2}$. 直线MN表示一条河流的河岸,在河流同旁有A、B两个村庄,现要在河边修建一个供水站给A、B供水.问:这个供水站建在什么地方,可以使铺设管道最短?请在图中找出表示供水站的点P.
直线MN表示一条河流的河岸,在河流同旁有A、B两个村庄,现要在河边修建一个供水站给A、B供水.问:这个供水站建在什么地方,可以使铺设管道最短?请在图中找出表示供水站的点P. 如图,已知l1∥l2,l3和直线l1,l2分别交于A、B两点,点P在直线AB.
如图,已知l1∥l2,l3和直线l1,l2分别交于A、B两点,点P在直线AB.