题目内容
19.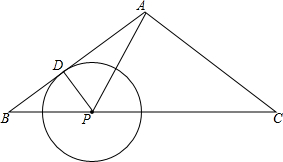 如图,在△ABC中,AB=AC=10,BC=16,点P为BC边上的一个动点,以P为圆心的⊙P与边AB相切于点D.在点P移动的过程中,△APC如果成为等腰三角形,求⊙P的半径.
如图,在△ABC中,AB=AC=10,BC=16,点P为BC边上的一个动点,以P为圆心的⊙P与边AB相切于点D.在点P移动的过程中,△APC如果成为等腰三角形,求⊙P的半径.
分析 作AH⊥BC于H,利用等腰三角形的性质和勾股定理计算出AH,再利用切线的性质得PD⊥AB,然后分类讨论:当CP=CA=10时,如图1,则BP=BC-CP=6,通过证明Rt△BPD∽Rt△BAH,利用相似比克计算出PD;当PA=PC时,作PE⊥AC于E,如图2,则AE=CE=5,先利用△CPE∽△CAH,通过相似比计算出CP,从而得到BP的长,接着利用Rt△BPD∽Rt△BAH,通过相似比计算PD的长.
解答 解:作AH⊥BC于H,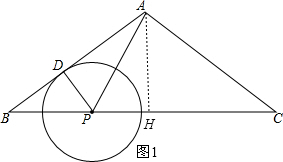
∵AB=AC=10,
∴BH=CH=$\frac{1}{2}$BC=8,
∴AH=$\sqrt{{10}^{2}-{8}^{2}}$=6,
∵AB与⊙P相切,
∴PD⊥AB,
当CP=CA=10时,如图1,BP=BC-CP=6,
∵∠PBD=∠ABH,
∴Rt△BPD∽Rt△BAH,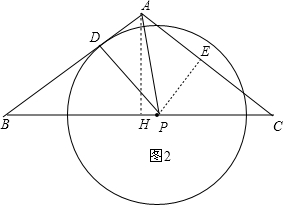
∴$\frac{DP}{AH}$=$\frac{BP}{AB}$,即$\frac{PD}{6}$=$\frac{6}{10}$,解得PD=$\frac{18}{5}$;
当PA=PC时,作PE⊥AC于E,如图2,则AE=CE=5,
易证得△CPE∽△CAH,
∴$\frac{CP}{AC}$=$\frac{CE}{CH}$,即$\frac{CP}{10}$=$\frac{5}{8}$,解得CP=$\frac{25}{4}$,
∴BP=16-$\frac{25}{4}$=$\frac{39}{4}$,
∵∠PBD=∠ABH,
∴Rt△BPD∽Rt△BAH,
∴$\frac{DP}{AH}$=$\frac{BP}{AB}$,即$\frac{PD}{6}$=$\frac{\frac{39}{4}}{10}$,解得PD=$\frac{117}{20}$,
综上所述,⊙P的半径为$\frac{18}{5}$或$\frac{117}{20}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.解决本题的关键灵活运用等腰三角形的性质和相似比计算线段的长.

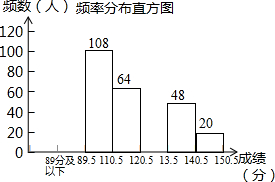 某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:
某县为调查九年级15000名学生“一模”考试的数学成绩的分布情况,抽取了400名学生的数学成绩(成绩得分皆为整数,满分150分)进行统计:频率分布表
| 分组 | 频数 | 频率 |
| 89分及以下 | ||
| 89.5-110.5 | 108 | |
| 110.5-120.5 | 64 | 0.16 |
| 120.5-130.5 | 0.20 | |
| 130.5-140.5 | 48 | |
| 140.5-150.5 | 20 | 0.05 |
| 合计 | 400 | 1 |
(1)补全频率分布表;
(2)补全频数分布直方图;
(3)若将得分转化为等级,规定得分“89分及以下”分评为“D”,“89.5-110.5分”评为“C”,“110.5-130.5扥”评为“B”,“130.5-150.5分”评为“A”,这次15000名学生中约有多少人评为“D”?如果随机抽取一名学生的成绩等级,则这名学生的成绩评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由.
| A. | a8÷a4=a4 | B. | (-a)5÷(-a)4=-a | C. | (-a)5÷(-a4)=a | D. | (b-a)3÷(a-b)2=a-b |
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
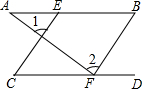 如图,已知∠1=∠2,∠B=∠C,试说明AB∥CD.
如图,已知∠1=∠2,∠B=∠C,试说明AB∥CD. 如图,已知l1∥l2,l3和直线l1,l2分别交于A、B两点,点P在直线AB.
如图,已知l1∥l2,l3和直线l1,l2分别交于A、B两点,点P在直线AB.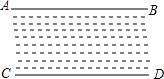 如图所示,直线AB,CD表示一条小河的两条河岸线,小明和小刚想利用数学知识判断这里两条河岸线是否平行,两人现在分别在小河的两侧,每人手中各有两根标杆和一个测角仪,请你帮他们想象办法.
如图所示,直线AB,CD表示一条小河的两条河岸线,小明和小刚想利用数学知识判断这里两条河岸线是否平行,两人现在分别在小河的两侧,每人手中各有两根标杆和一个测角仪,请你帮他们想象办法.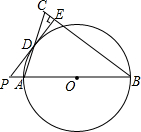 如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P.
如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P.