题目内容
18. 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示的数为-$\sqrt{2}$,设点B所表示的数为n.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示的数为-$\sqrt{2}$,设点B所表示的数为n.(1)求n的值;
(2)求|n+1|+2(n+2$\sqrt{2}$-2)-1的值.
分析 (1)根据数轴上的点运动规律:右加左减的规律可求出n的值;
(2)把n的值代入,再根据绝对值的性质、负整数指数幂的计算法则计算即可得解.
解答 解:(1)∵蚂蚁从点A沿数轴向右直爬2个单位到达点B,
∴点B所表示的数比点A表示的数大2,
∵点A表示-$\sqrt{2}$,点B所表示的数为n,
∴n=-$\sqrt{2}$+2;
(2)|n+1|+2(n+2$\sqrt{2}$-2)-1
=|-$\sqrt{2}$+2+1|+2×(-$\sqrt{2}$+2+2$\sqrt{2}$-2)-1
=-$\sqrt{2}$+3+2×$\frac{\sqrt{2}}{2}$
=-$\sqrt{2}$+3+$\sqrt{2}$
=3.
点评 本题考查了实数与数轴,是基础题,主要利用了在数轴上向右移动加的规律,还利用了绝对值的性质、负整数指数幂和二次根式的运算.

练习册系列答案
相关题目
9.下列运算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{3}$×($\sqrt{8}$-$\sqrt{2}$)=$\sqrt{3}$×$\sqrt{6}$=$\sqrt{18}$ | C. | $\sqrt{9}$=±3 | D. | |$\sqrt{5}$-$\sqrt{7}$|=$\sqrt{7}$-$\sqrt{5}$ |
10.下列给出的数轴中正确的是( )
| A. |  | B. |  | C. |  | D. |  |
 有理数m,n在数轴上的位置如图所示,化简$\sqrt{{m}^{2}}$-$\sqrt{{n}^{2}}$-$\sqrt{(m-n)^{2}}$=-2n.
有理数m,n在数轴上的位置如图所示,化简$\sqrt{{m}^{2}}$-$\sqrt{{n}^{2}}$-$\sqrt{(m-n)^{2}}$=-2n.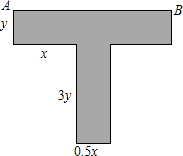 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求: 如图,已知△ABC≌△ADE,∠C=79°,DE⊥AB,则∠D的度数为68°.
如图,已知△ABC≌△ADE,∠C=79°,DE⊥AB,则∠D的度数为68°.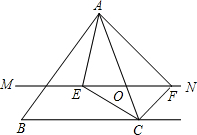 △ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠DCA的平分线于点F.
△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠DCA的平分线于点F.