题目内容
9.下列运算正确的是( )| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{3}$×($\sqrt{8}$-$\sqrt{2}$)=$\sqrt{3}$×$\sqrt{6}$=$\sqrt{18}$ | C. | $\sqrt{9}$=±3 | D. | |$\sqrt{5}$-$\sqrt{7}$|=$\sqrt{7}$-$\sqrt{5}$ |
分析 利用二次根式的加减法对A进行判断;根据二次根式的乘法法则对B进行判断;根据算术平方根的定义对C进行判断;根据绝对值的意义对D进行判断.
解答 解:A、$\sqrt{2}$与$\sqrt{3}$不能合并,然后A选项错误;
B、原式=$\sqrt{3}$(2$\sqrt{2}$-$\sqrt{2}$)=$\sqrt{3}$×$\sqrt{2}$=$\sqrt{3×2}$=$\sqrt{6}$,所以B选项错误;
C、原式=3,所以C选项错误;
D、原式=$\sqrt{7}$-$\sqrt{5}$,所以D选项正确.
故选D.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
19.用代数式表示:“x的5倍与y的和的一半”可以表示为( )
| A. | 5x+$\frac{1}{2}$y | B. | $\frac{1}{2}$ (5x+y) | C. | $\frac{1}{2}$(5x+2y) | D. | 5x+y. |
20.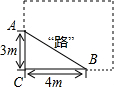 如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB,爱心小组想在A处树立一个标牌“少走■米,踏之何刃?”请你计算后帮她们在标牌的■填上适当的数字为2米.
如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB,爱心小组想在A处树立一个标牌“少走■米,踏之何刃?”请你计算后帮她们在标牌的■填上适当的数字为2米.
 如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB,爱心小组想在A处树立一个标牌“少走■米,踏之何刃?”请你计算后帮她们在标牌的■填上适当的数字为2米.
如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB,爱心小组想在A处树立一个标牌“少走■米,踏之何刃?”请你计算后帮她们在标牌的■填上适当的数字为2米.
14.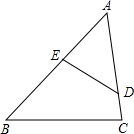 如图,下列条件不能判定△ABC与△ADE相似的是( )
如图,下列条件不能判定△ABC与△ADE相似的是( )
 如图,下列条件不能判定△ABC与△ADE相似的是( )
如图,下列条件不能判定△ABC与△ADE相似的是( )| A. | $\frac{AE}{AC}$=$\frac{DE}{BC}$ | B. | ∠B=∠ADE | C. | $\frac{AE}{AD}$=$\frac{AC}{AB}$ | D. | ∠C=∠AED |
1.下列语句正确的是( )
| A. | 1+a不是一个代数式 | |
| B. | 0是一个单项式 | |
| C. | 一个多项式的次数为5,那么这个多项式的各项的次数都小于5 | |
| D. | 单项式-$\frac{2πa{b}^{2}}{3}$的系数是-$\frac{2}{3}$ |
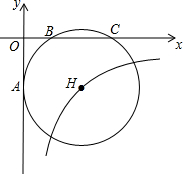 如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则反比例函数的解析式为-8$\sqrt{3}$.
如图所示,经过B(2,0)、C(6,0)两点的⊙H与y轴的负半轴相切于点A,双曲线y=$\frac{k}{x}$经过圆心H,则反比例函数的解析式为-8$\sqrt{3}$.
 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示的数为-$\sqrt{2}$,设点B所表示的数为n.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示的数为-$\sqrt{2}$,设点B所表示的数为n.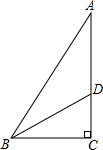 如图,在 Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若CD=3cm,则点D到AB的距离是3cm..
如图,在 Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若CD=3cm,则点D到AB的距离是3cm..