Question

1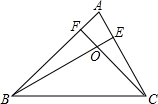．已知：如图，△ABC的两条高线BE，CF相交于点O．求证：∠BOC=180°-∠A（填空）．
证明：∵BE，CF是△ABC的两条高线（已知），
∴∠OEC=∠BFC=90°（高线的定义）．
∵∠ACF+∠A=∠BFC=90°（直角三角形的性质），
∴∠ACF=90°-∠A．
∴∠BOC=∠OEC+∠ACF=90°+90°-∠A=180°-∠A．

Answer 1

分析 由三角形的高线得出∠OEC=∠BFC=90°，由直角三角形的性质得出∠ACF+∠A=90°，再由三角形的外角性质即可得出结论．

解答 解：∵BE，CF是△ABC的两条高线（已知），
∴∠OEC=∠BFC=90°（高线的定义）．
∵∠ACF+∠A=∠BFC=90°（直角三角形的性质），
∴∠ACF=90°-∠A．
∴∠BOC=∠OEC+∠ACF=90°+90°-∠A=180°-∠A．
故答案为：已知，高线的定义，直角三角形的性质．

点评 本题考查了三角形内角和定理、直角三角形的性质、三角形的外角性质；熟练掌握三角形内角和定理，并能进行推理论证是解决问题的关键．