题目内容
 某几何体的展开图如图所示:
某几何体的展开图如图所示:(1)这个几何体的名称是
(2)画出这个几何体的三视图;
(3)若展开图的长是宽的2倍,求这个几何体的体积.(保留π)
考点:作图-三视图,几何体的展开图
专题:
分析:(1)由展开图可直接得到答案,此几何体为圆柱;
(2)圆柱的左视图与主视图都是长方形,俯视图是圆;
(3)根据圆柱体的体积公式=底面积×高计算即可.
(2)圆柱的左视图与主视图都是长方形,俯视图是圆;
(3)根据圆柱体的体积公式=底面积×高计算即可.
解答:解:(1)由展开图可得此几何体为圆柱;
(2)如图所示
 ;
;
(3)体积为:
πr2h=π×(20×2÷π÷2)2×20
=π×(
)2×20
=
.
故答案为:圆柱.
(2)如图所示
 ;
;(3)体积为:
πr2h=π×(20×2÷π÷2)2×20
=π×(
| 20 |
| π |
=
| 8000 |
| π |
故答案为:圆柱.
点评:此题主要考查了由展开图得几何体,以及画三视图,关键是考查同学们的空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
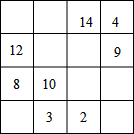 将1~16这16个整数填入4×4的正方形表格中,使得每行、每列、每条对角线上四个数之和都相等,如图所示,恰有8个小方格中填的数被一个淘气的小朋友擦掉了,请你将擦掉的这8个数设法恢复出来.
将1~16这16个整数填入4×4的正方形表格中,使得每行、每列、每条对角线上四个数之和都相等,如图所示,恰有8个小方格中填的数被一个淘气的小朋友擦掉了,请你将擦掉的这8个数设法恢复出来.