题目内容
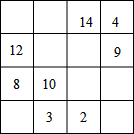将1～16这16个整数填入4×4的正方形表格中，使得每行、每列、每条对角线上四个数之和都相等，如图所示，恰有8个小方格中填的数被一个淘气的小朋友擦掉了，请你将擦掉的这8个数设法恢复出来．考点：有理数的加法
专题：
分析：利用1至16的和是136，136÷4=34，也就是每行数字或每列数字的和是34求解．
解答：解：1至16的和是136，136÷4=34，也就是每行数字或每列数字的和是34．
由第一行有14+4=18，还需要16，可用的只有5与11或1与15 两组，
两个数的位置，考虑到第一列原有两个数都比第二列大，所以选较小的在第一个位置．
第一次试5和11，发现第一列最下方必须用到9，而9已经存在了，只能将第一行的改为1与15这一组．
然后，就是将3个数字的，先补足为4个数字．
故答案为：1，15，6，7，11，5，16．
由第一行有14+4=18，还需要16，可用的只有5与11或1与15 两组，
两个数的位置，考虑到第一列原有两个数都比第二列大，所以选较小的在第一个位置．
第一次试5和11，发现第一列最下方必须用到9，而9已经存在了，只能将第一行的改为1与15这一组．
然后，就是将3个数字的，先补足为4个数字．
故答案为：1，15，6，7，11，5，16．
点评：本题主要考查了有理数的加法，解题的关键是求出第一行的数字．
练习册系列答案
相关题目
某几何体的展开图如图所示：若点M在第三象限，且M到x轴，y轴的距离均为2，则点M关于x轴对称点的坐标为（ ）
| A、（2.1） |
| B、（-2，2） |
| C、（2，-2） |
| D、（-2，-2） |
若点A关于y轴的对称点是A（
，1），则点A的坐标为（ ）
| 1 |
| 2 |
A、（
| ||
B、（1，
| ||
C、（-
| ||
D、（
|
如图，一根直立的旗杆高8米，一阵大风吹过，旗杆从点C处这段，顶部（B）着地，离旗杆底部（A）4米，工人在修复的过程中，发现在折断点C的下方1.25米D处，有一明显裂痕，若下次大风将旗杆从D处吹断，则距离杆脚周围多大范围内有被砸伤的危险？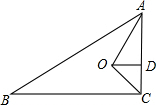
如图，在△ABC中，∠ACB=90°，AO、GO分别平分∠BAC和∠ACB，OD⊥AC于D．若AB=10，BC=8，试求线段OD的长度．
如图，A、B、C、D、E、都是⊙O上的点，AB=BC=CD，∠BCD=130°，求∠AED度数．