题目内容
7.(1)已知:在?ABCD中,对角线AC,BD相交于点O,∠BAC=90°,AB=AC,E为AB边上一点,连接CE,交OB于点P.①如图1,当E为AB中点,且AB=2时,PC的值为$\frac{2\sqrt{5}}{3}$;
②如图2,当$\frac{BE}{BA}$=$\frac{1}{4}$时,求tan∠OPC的值;
(2)如图3,在Rt△ABC中,∠A=90°,O为AC的中点,E为AB上一点,连接CE,交OB于点P,当BE:BA:CA=1:n:2$\sqrt{n}$时,tan∠OPC的值为$\frac{1}{2}$.
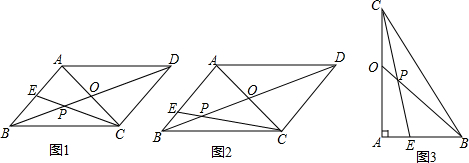
分析 (1)先根据勾股定理求出CE的长,再由AB∥CD得出△BPE∽△DPC,故可得出$\frac{PE}{PC}$=$\frac{1}{2}$,由此可得出PC的长;
(2)根据$\frac{BE}{BA}$=$\frac{1}{4}$得出BE的长,同(1)可得CE的长及△BPE∽△DPC,故可得出$\frac{PE}{PC}$=$\frac{1}{4}$,由此得出PE的长,故可得出BE=PE,再由锐角三角函数的定义即可得出结论;
(3)作CF∥AB交BO的延长线于点F,过点C作CQ⊥BF于点Q,设BE=x,则AB=nx,OA=OC=$\sqrt{n}$x,根据勾股定理求出OB的长,由ASAA定理得出△OAB≌△OCF,根据三角形的面积公式得出CQ的长,再求出FQ的长,由△PCF∽△PEB可得出PB的长,再求出PQ的长,根据锐角三角函数的定义即可得出结论.
解答 解:(1)∵∠BAC=90°,AB=AC,E为AB中点,且AB=2,
∴AE=BE=1,CE=$\sqrt{{AE}^{2}+{AC}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=2,
∴∠EBP=∠CDP,
∴△EBP∽△CDP,
∴$\frac{EP}{PC}$=$\frac{BE}{CD}$,即$\frac{EP}{PC}$=$\frac{1}{2}$,
∴PC=$\frac{1}{3}$CE=$\frac{2\sqrt{5}}{3}$.
故答案为:$\frac{2\sqrt{5}}{3}$;
(2)设AB=CD=AC=4a,
∵$\frac{BE}{BA}$=$\frac{1}{4}$,
∴BE=a.
∵∠BAC=90°,AB=AC,
∴CE=$\sqrt{{AE}^{2}+{AC}^{2}}$=$\sqrt{{(3a)}^{2}+{(4a)}^{2}}$=5a.
同(1)可得△EBP∽△CDP,
∴$\frac{EP}{PC}$=$\frac{BE}{CD}$,即$\frac{EP}{PC}$=$\frac{a}{4a}$=$\frac{1}{4}$,
∴EP=a,
∴BE=EP,
∴∠EBP=∠EPB=∠OPC.
∵四边形ABCD是平行四边形,∠BAC=90°,
∴OA=$\frac{1}{2}$AC=2a,
∴tan∠OPC=tan∠EBP=$\frac{OA}{AB}$=$\frac{2a}{4a}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$;
(3)如图,作CF∥AB交BO的延长线于点F,过点C作CQ⊥BF于点Q,
∵BE:BA:CA=1:n:2$\sqrt{n}$,O为AC的中点,
∴设BE=x,则AB=nx,OA=OC=$\sqrt{n}$x,
∴OB=$\sqrt{{OA}^{2}+{AB}^{2}}$=$\sqrt{{(\sqrt{n}x)}^{2}+{(nx)}^{2}}$=$\sqrt{n+{n}^{2}}$x.
∵CF∥AB,∠A=90°,
∴∠A=∠OCF=90°.
在△OAB与△OCF中,
∵$\left\{\begin{array}{l}∠A=∠OCF\\ OA=OC\\∠AOB=∠COF\end{array}\right.$,
∴△OAB≌△OCF(ASA),
∴CF=AB=nx,OF=OB=$\sqrt{n+{n}^{2}}$x,BF=2OF,
∴CQ=$\frac{CF•OC}{OF}$=$\frac{nx•\sqrt{n}x}{x\sqrt{n+{n}^{2}}}$=$\frac{n\sqrt{n}x}{\sqrt{n+{n}^{2}}}$,
∴FQ=$\sqrt{{CF}^{2}-{CQ}^{2}}$=$\sqrt{{(nx)}^{2}-{(\frac{nx\sqrt{n}}{\sqrt{n+{n}^{2}}})}^{2}}$=nx$\sqrt{\frac{n}{n+1}}$.
∵CF∥AB,
∴∠PCF=∠=∠PEB,
∴△PCF∽△PEB,
∴$\frac{PB}{PF}$=$\frac{BE}{CF}$,即$\frac{PB}{PF}$=$\frac{x}{nx}$=$\frac{1}{n}$,
∵PB+PF=2x$\sqrt{n+{n}^{2}}$,
∴PB=$\frac{2x\sqrt{n+{n}^{2}}}{n+1}$,
∴PQ=BF-FQ-PB=2x$\sqrt{n+{n}^{2}}$-nx$\sqrt{\frac{n}{n+1}}$-$\frac{2x\sqrt{n+{n}^{2}}}{n+1}$=$\frac{nx\sqrt{n(n+1)}}{n+1}$,
∴tan∠OPC=$\frac{QC}{PQ}$=$\frac{\frac{nx\sqrt{n}}{\sqrt{n+{n}^{2}}}}{\frac{nx\sqrt{n(n+1)}}{n+1}}$=$\frac{\sqrt{n}}{n}$.
点评 本题考查的是相似形综合题,涉及到相似三角形的判定与性质、平行四边形的性质及全等三角形的判定与性质、勾股定理等知识,难度较大,在解答(3)时要注意作出辅助线,构造出全等三角形求解.

 阅读快车系列答案
阅读快车系列答案| 同学 | 红球 | 白球 | 黑球 |
| 甲 | 1 | 5 | |
| 乙 | 3 | 7 | |
| 丙 |
(2)如果你是丙同学,请把你的实验结果填写完整;
(3)比较每位同学的实验结果,哪位同学摸出红球的可能性最大?哪位同学摸出黑球的可能性最大?
(4)三位同学所做的实验中,事件“摸到红球”的可能性,事件“摸到白球”的可能性,事件“摸到黑球”的可能性分别是多少,这三个事件的可能性之和是多少?
 实验与探究:
实验与探究: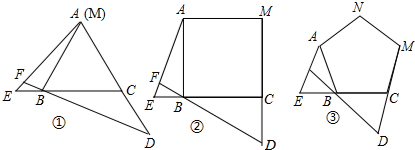
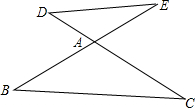 如图,AB•AE=AC•AD,若∠C=25°,则∠E的度数是25°.
如图,AB•AE=AC•AD,若∠C=25°,则∠E的度数是25°.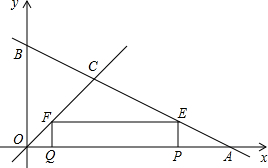 如图所示,直线y=-$\frac{1}{2}x$+4与坐标轴分别交于点A、B,与直线y=x交于点C,在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A作匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形总为矩形(点P、Q重合除外).
如图所示,直线y=-$\frac{1}{2}x$+4与坐标轴分别交于点A、B,与直线y=x交于点C,在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A作匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形总为矩形(点P、Q重合除外).