题目内容
8．
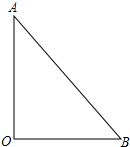如图所示，某探险队的A组由驻地O点出发，以12km/h的速度前进，同时，B组也由驻地O出发，以9km/h的速度向另一个方向前进，2h后同时停下来，这时A，B两组相距30km．（1）此时，A，B两组行进的方向成直角吗？请说明理由；
（2）若A，B两组仍以原速前进，相向而行，经过几小时后相遇？
分析 （1）根据题意可以知道OB和OA的长度，又知A和B的距离，利用勾股定理的逆定理判定三角形的形状；
（2）要想最快相遇，则必须相向而行，由此根据路程÷速度和=相遇时间得出答案即可．
解答 解：（1）出发2小时，A组行了12×2=24千米，B组行了9×2=18千米，
这时A，B两组相距30千米，
且有242+182=302，
所以A，B两组行进的方向成直角．
（2）若A，B两组仍以原速前进，要想最快相遇，则必须相向而行，
所以至少30÷（12+9）=$\frac{10}{7}$小时相遇．
点评 此题考查勾股定理的逆定理的实际运用，结合图形，理解题意，解决问题．
练习册系列答案
阅读快车系列答案
相关题目
19．一个口袋里装有除颜色外，形状、大小，质量均相同的若干个小球，其中红球1个，白球有3个，黑球有6个，甲、乙、丙三位同学分别做同一实验：把口袋里的球搅匀后，摸出一个球来，记下颜色后，将球放回袋中，再次重复，共进行10次，下表是记录的结果：
（1）请把甲、乙两位同学的记录补充完整；
（2）如果你是丙同学，请把你的实验结果填写完整；
（3）比较每位同学的实验结果，哪位同学摸出红球的可能性最大？哪位同学摸出黑球的可能性最大？
（4）三位同学所做的实验中，事件“摸到红球”的可能性，事件“摸到白球”的可能性，事件“摸到黑球”的可能性分别是多少，这三个事件的可能性之和是多少？
| 同学 | 红球 | 白球 | 黑球 |
| 甲 | 1 | 5 | |
| 乙 | 3 | 7 | |
| 丙 |
（2）如果你是丙同学，请把你的实验结果填写完整；
（3）比较每位同学的实验结果，哪位同学摸出红球的可能性最大？哪位同学摸出黑球的可能性最大？
（4）三位同学所做的实验中，事件“摸到红球”的可能性，事件“摸到白球”的可能性，事件“摸到黑球”的可能性分别是多少，这三个事件的可能性之和是多少？
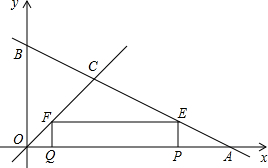如图所示，直线y=-$\frac{1}{2}x$+4与坐标轴分别交于点A、B，与直线y=x交于点C，在线段OA上，动点Q以每秒1个单位长度的速度从点O出发向点A作匀速运动，同时动点P从点A出发向点O做匀速运动，当点P、Q其中一点停止运动时，另一点也停止运动．分别过点P、Q作x轴的垂线，交直线AB、OC于点E、F，连接EF．若运动时间为t秒，在运动过程中四边形总为矩形（点P、Q重合除外）．
3．以下列各组线段为边，不能构成三角形的是（ ）
| A． | $\sqrt{2}$，$\sqrt{3}$，1 | B． | 3，4，5 | C． | 2，7，9 | D． | $\frac{3}{2}$，3，$\frac{5}{2}$ |