题目内容
14.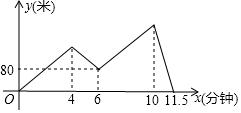 甲、乙两人沿着一条笔直的公路进行长跑比赛,两人同时同地同向起跑,甲匀速跑完全程,并始终领先乙,甲到终点后原地休息.乙先匀速跑了4分钟后将速度提高至原来的1.5倍,再经过2分钟,乙又将速度降低至出发时的速度,并以这一速度完成余下的比赛.甲、乙两人的距离y(米)与乙出发的时间x(分钟)之间的关系如图所示,则比赛的全程为2000米.
甲、乙两人沿着一条笔直的公路进行长跑比赛,两人同时同地同向起跑,甲匀速跑完全程,并始终领先乙,甲到终点后原地休息.乙先匀速跑了4分钟后将速度提高至原来的1.5倍,再经过2分钟,乙又将速度降低至出发时的速度,并以这一速度完成余下的比赛.甲、乙两人的距离y(米)与乙出发的时间x(分钟)之间的关系如图所示,则比赛的全程为2000米.
分析 设甲的速度为x米/分钟,乙初始速度为y米/分钟,则比赛的全程为10x米,观察函数图象,找出关于x、y的二元一次方程组,解之即可得出x的值,将其代入10x中即可得出比赛全程的长度.
解答 解:设甲的速度为x米/分钟,乙初始速度为y米/分钟,则比赛的全程为10x米,
根据题意得:$\left\{\begin{array}{l}{6x=4y+2×1.5y+80}\\{(11.5-2)y+2×1.5y=10x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=200}\\{y=160}\end{array}\right.$,
∴10x=2000.
故答案为:2000.
点评 本题考查了二元一次方程组的应用以及一次函数图象,观察函数图象,列出关于x、y的二元一次方程组是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图,在四边形ABCD中,对角线AC、BD相交于点O,AD∥BC,添加下列条件不能使四边形ABCD成为平行四边形的是( )
如图,在四边形ABCD中,对角线AC、BD相交于点O,AD∥BC,添加下列条件不能使四边形ABCD成为平行四边形的是( )
 如图,在四边形ABCD中,对角线AC、BD相交于点O,AD∥BC,添加下列条件不能使四边形ABCD成为平行四边形的是( )
如图,在四边形ABCD中,对角线AC、BD相交于点O,AD∥BC,添加下列条件不能使四边形ABCD成为平行四边形的是( )| A. | AD=BC | B. | OA=OC | C. | ∠ABC+∠BCD=180° | D. | AB=CD |
 某商场为了吸引顾客,设立一个可以自由转动的转盘(如图,转盘被平分成20份),并规定:顾客每购物满200元就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,甲顾客购物220元,他获得购物卷的概率是多少?他获得20元购物券的概率是多少?
某商场为了吸引顾客,设立一个可以自由转动的转盘(如图,转盘被平分成20份),并规定:顾客每购物满200元就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,甲顾客购物220元,他获得购物卷的概率是多少?他获得20元购物券的概率是多少?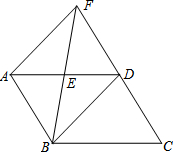 如图,在?ABCD中,点E是边AD的中点,射线BE交CD的延长线于点F,连接AF,BD
如图,在?ABCD中,点E是边AD的中点,射线BE交CD的延长线于点F,连接AF,BD 如图,在?ABCD中,AE=CF.
如图,在?ABCD中,AE=CF. 如图,直线l1∥l2,被直线l所截,如果∠1=60°,那么∠2的度数为120°.
如图,直线l1∥l2,被直线l所截,如果∠1=60°,那么∠2的度数为120°.