题目内容
4.(1)解不等式组$\left\{\begin{array}{l}{x+1>0}\\{x≤\frac{x-2}{3}+2}\end{array}\right.$,并在数轴上表示它的解集.(2)解分式方程:$\frac{x}{x-2}$-1=$\frac{1}{x}$.
分析 (1)分别求出各个不等式的解集,再求出这些解集的公共部分并在数轴上表示出来即可.
(2)观察可得最简公分母是x(x-2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
解答 解:(1)$\left\{\begin{array}{l}{x+1>0①}\\{x≤\frac{x-2}{3}+2②}\end{array}\right.$,
解不等式①得x>-1,
解不等式②得x≤2,
所以不等式的解集是-1<x≤2,
如图所示:
(2)$\frac{x}{x-2}$-1=$\frac{1}{x}$,
x2-x(x-2)=x-2,
x2-x2+2x=x-2,
x=-2,
检验:当x=-2时,x(x-2)≠0,
故原分式方程的解是x=-2.
点评 考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.同时考查了解一元一次不等式组.

练习册系列答案
相关题目
 已知等腰直角三角形ABC中,∠A=90°,AB=AC=4,点D是AB边的中点,P为底边BC上一动点,以PD为边作∠DPQ=45°,且另一边PQ交线段AC于点Q,当△BDP为等腰三角形时,CQ=4或3或4$\sqrt{2}$-2.
已知等腰直角三角形ABC中,∠A=90°,AB=AC=4,点D是AB边的中点,P为底边BC上一动点,以PD为边作∠DPQ=45°,且另一边PQ交线段AC于点Q,当△BDP为等腰三角形时,CQ=4或3或4$\sqrt{2}$-2. 有一块长20cm,宽10cm的长方形铁片,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为96cm2的无盖的盒子,则这个盒子的容积为192cm3.
有一块长20cm,宽10cm的长方形铁片,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为96cm2的无盖的盒子,则这个盒子的容积为192cm3. 如图所示,AB=AC=5,BC=2,AB的垂直平分线MN交AC于点D,则△DBC的周长等于( )
如图所示,AB=AC=5,BC=2,AB的垂直平分线MN交AC于点D,则△DBC的周长等于( ) 如图,在△ABC,∠ACB=90°,∠ABC=15°,AB的中垂线DE交BC于D,E为垂足,若BD=8cm,则AC等于4cm.
如图,在△ABC,∠ACB=90°,∠ABC=15°,AB的中垂线DE交BC于D,E为垂足,若BD=8cm,则AC等于4cm. 某天早上6点,李老师从学校出发,乘车赶往市里开会,8点准时到达会场,开完会立即返回,中午12点回到学校,他记录下从早上6点到中午12点这段时间里他离学校的距离s(km)与时间t(h)之间的关系并画出如图所示的图象,根据图象提供的信息回答下列问题:
某天早上6点,李老师从学校出发,乘车赶往市里开会,8点准时到达会场,开完会立即返回,中午12点回到学校,他记录下从早上6点到中午12点这段时间里他离学校的距离s(km)与时间t(h)之间的关系并画出如图所示的图象,根据图象提供的信息回答下列问题: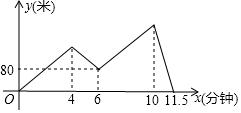 甲、乙两人沿着一条笔直的公路进行长跑比赛,两人同时同地同向起跑,甲匀速跑完全程,并始终领先乙,甲到终点后原地休息.乙先匀速跑了4分钟后将速度提高至原来的1.5倍,再经过2分钟,乙又将速度降低至出发时的速度,并以这一速度完成余下的比赛.甲、乙两人的距离y(米)与乙出发的时间x(分钟)之间的关系如图所示,则比赛的全程为2000米.
甲、乙两人沿着一条笔直的公路进行长跑比赛,两人同时同地同向起跑,甲匀速跑完全程,并始终领先乙,甲到终点后原地休息.乙先匀速跑了4分钟后将速度提高至原来的1.5倍,再经过2分钟,乙又将速度降低至出发时的速度,并以这一速度完成余下的比赛.甲、乙两人的距离y(米)与乙出发的时间x(分钟)之间的关系如图所示,则比赛的全程为2000米.