题目内容
19. 如图,在?ABCD中,AE=CF.
如图,在?ABCD中,AE=CF.(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为平行四边形.
分析 (1)由四边形ABCD是平行四边形,推出AD=BC,∠A=∠C,再根据SAS即可证明;
(2)只要证明DF=BE,DF∥BE即可;
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
在△ADE和△CBF中,
$\left\{\begin{array}{l}{AD=BC}\\{∠A=∠C}\\{AE=CF}\end{array}\right.$,
∴△ADE≌△CBF(SAS).
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AE=CF,
∴DF=EB,
∵DF∥EB,
∴四边形BFDE是平行四边形.
点评 本题考查平行四边形的判定和性质、全等三角形的判定等知识,解题的关键是正确寻找全等三角形的全等条件,灵活运用所学知识解决问题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
10.下列条件中,不能判定一个四边形是平行四边形的是( )
| A. | 两组对边分别平行 | B. | 一组对边平行且相等 | ||
| C. | 一组对边相等且一组对角相等 | D. | 两组对角分别相等 |
 如图所示,AB=AC=5,BC=2,AB的垂直平分线MN交AC于点D,则△DBC的周长等于( )
如图所示,AB=AC=5,BC=2,AB的垂直平分线MN交AC于点D,则△DBC的周长等于( )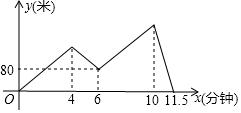 甲、乙两人沿着一条笔直的公路进行长跑比赛,两人同时同地同向起跑,甲匀速跑完全程,并始终领先乙,甲到终点后原地休息.乙先匀速跑了4分钟后将速度提高至原来的1.5倍,再经过2分钟,乙又将速度降低至出发时的速度,并以这一速度完成余下的比赛.甲、乙两人的距离y(米)与乙出发的时间x(分钟)之间的关系如图所示,则比赛的全程为2000米.
甲、乙两人沿着一条笔直的公路进行长跑比赛,两人同时同地同向起跑,甲匀速跑完全程,并始终领先乙,甲到终点后原地休息.乙先匀速跑了4分钟后将速度提高至原来的1.5倍,再经过2分钟,乙又将速度降低至出发时的速度,并以这一速度完成余下的比赛.甲、乙两人的距离y(米)与乙出发的时间x(分钟)之间的关系如图所示,则比赛的全程为2000米.