题目内容
3．已知ax2+bx+1与2x2-3x+1的积不含x3项，也不含x项，求a与b的值．分析 由题意列出算式，利用多项式乘以多项式法则计算，合并后令三次项与一次项系数为0，即可求出a与b的值．
解答 解：根据题意列得：（ax2+bx+1）（2x2-3x+1）=2ax4+（2b-3a）x3+（a+2-3b）x2+（b-3）x+1，
∵不含x3的项，也不含x的项，
∴2b-3a=0，b-3=0，
解得a=2，b=3．
点评 此题考查了多项式乘以多项式，熟练掌握多项式乘以多项式法则是解本题的关键．
练习册系列答案
相关题目
某天早上6点，李老师从学校出发，乘车赶往市里开会，8点准时到达会场，开完会立即返回，中午12点回到学校，他记录下从早上6点到中午12点这段时间里他离学校的距离s（km）与时间t（h）之间的关系并画出如图所示的图象，根据图象提供的信息回答下列问题：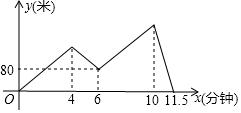
甲、乙两人沿着一条笔直的公路进行长跑比赛，两人同时同地同向起跑，甲匀速跑完全程，并始终领先乙，甲到终点后原地休息．乙先匀速跑了4分钟后将速度提高至原来的1.5倍，再经过2分钟，乙又将速度降低至出发时的速度，并以这一速度完成余下的比赛．甲、乙两人的距离y（米）与乙出发的时间x（分钟）之间的关系如图所示，则比赛的全程为2000米．
15．一次函数y=kx+1的图象必过点（ ）
| A． | （0，1） | B． | （0，-1） | C． | （1，0） | D． | （-1，0） |
13．下列计算正确的是（ ）
| A． | a4+a5=a9 | B． | a3•a3•a3=3x3 | C． | （-a3）4=a7 | D． | 2a4•3a5=6a9 |