题目内容
2．已知关于x，y的二元一次方程组$\left\{\begin{array}{l}{4x+y=k+2}\\{x+4y=3}\end{array}\right.$的解满足0＜x+y＜1，则k的取值范围是-5＜k＜0．分析 将两方程相加整理可得x+y=$\frac{k+5}{5}$，由0＜x+y＜1可得0＜$\frac{k+5}{5}$＜1，解之即可得．
解答 解：将两方程相加可得5x+5y=k+5，
∴x+y=$\frac{k+5}{5}$，
∵0＜x+y＜1，
∴0＜$\frac{k+5}{5}$＜1，
解得：-5＜k＜0，
故答案为：-5＜k＜0．
点评 本题主要考查解一元一次不等式组和二元一次方程组，根据题意得出关于k的不等式组是解题的关键．
练习册系列答案
相关题目
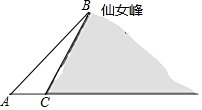数学“综合与实践”课中，老师带领同学们来到娄底市郊区，测算如图所示的仙女峰的高度，李红盛同学利用已学的数学知识设计了一个实践方案，并实施了如下操作：先在水平地面A处测得山顶B的仰角∠BAC为38.7°，再由A沿水平方向前进377米到达山脚C处，测得山坡BC的坡度为1：0.6，请你求出仙女峰的高度（参考数据：tan38.7°≈0.8）
如图，?ABCD中，∠B=45°，AC⊥BC，E是CA延长线上一点，O是AB的中点，连接OE，交DA延长线与点H，过点O作OG⊥OE交AC于点F，交BC的延长线于点G，连接CO．
如图，抛物线y=ax2+bx-3（a≠0）与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，且BO=OC=3AO．