题目内容
12. 如图,抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且BO=OC=3AO.
如图,抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且BO=OC=3AO.(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的点P坐标;若不存在,请说明理由.
分析 (1)先求出点C的坐标,在由BO=OC=3AO,确定出点B,A的坐标,最后用待定系数法求出抛物线解析式;
(2)设出点P的坐标,表示出PB,PC,求出BC,分三种情况利用两边相等建立方程求解即可.
解答 解:(1)∵抛物线y=ax2+bx-3,
∴c=-3,
∴C(0,-3),
∴OC=3,
∵BO=OC=3AO,
∴BO=3,AO=1,
∴B(3,0),A(-1,0),
∵该抛物线与x轴交于A、B两点,
∴$\left\{\begin{array}{l}{9a+3b-3=0}\\{a-b-3=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
∴抛物线解析式为y=x2-2x-3,
(2)存在,
理由:设P(1,m),
∵B(3,0),C(0,-3),
∴BC=3$\sqrt{2}$,PB=$\sqrt{{m}^{2}+4}$,PC=$\sqrt{(m+3)^{2}+1}$,
∵△PBC是等腰三角形,
①当PB=PC时,
∴$\sqrt{{m}^{2}+4}$=$\sqrt{(m+3)^{2}+1}$,
∴m=-1,
∴P(1,-1),
②当PB=BC时,
∴3$\sqrt{2}$=$\sqrt{{m}^{2}+4}$,
∴m=±$\sqrt{14}$,
∴P(1,$\sqrt{14}$)或P(1,-$\sqrt{14}$),
③当PC=BC时,
∴3$\sqrt{2}$=$\sqrt{(m+3)^{2}+1}$,
∴m=-3±$\sqrt{17}$,
∴P(1,-3+$\sqrt{17}$)或P(1,-3-$\sqrt{17}$),
∴符合条件的P点坐标为P(1,-1)或P(1,$\sqrt{14}$)或P(1,-$\sqrt{14}$)或P(1,-3+$\sqrt{17}$)或P(1,-3-$\sqrt{17}$).
点评 此题是二次函数综合题,主要考查了待定系数法,等腰三角形的性质,解本题的关键是用方程的思想解决问题.

| A. | a(x1-x2)=k | B. | a(x2-x1)=k | C. | a(x1-x2)2=k | D. | a(x1+x2)2=k |
| A. | -2与$\sqrt{(-2)^{2}}$ | B. | 0与π-3.14 | C. | 8与$\root{3}{-64}$ | D. | 6与$\sqrt{(-6)^{2}}$ |

 如图,是由6个正方体组成的图案,请分别画出从三个方向看到的形状图.
如图,是由6个正方体组成的图案,请分别画出从三个方向看到的形状图.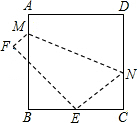 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则$\frac{AM}{CN}$的值是$\frac{1}{3}$.
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则$\frac{AM}{CN}$的值是$\frac{1}{3}$.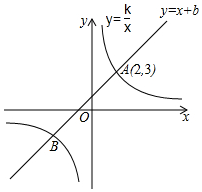 如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).
如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).