题目内容
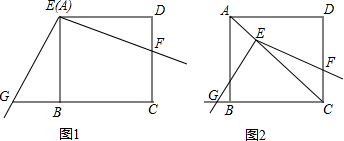
17. 如图,?ABCD中,∠B=45°,AC⊥BC,E是CA延长线上一点,O是AB的中点,连接OE,交DA延长线与点H,过点O作OG⊥OE交AC于点F,交BC的延长线于点G,连接CO.
如图,?ABCD中,∠B=45°,AC⊥BC,E是CA延长线上一点,O是AB的中点,连接OE,交DA延长线与点H,过点O作OG⊥OE交AC于点F,交BC的延长线于点G,连接CO.(1)若CD=4,求四边形AHOF的面积;
(2)若∠COF=15°,求证:BG-AH=2OF.
分析 (1)由条件可证得△OAH≌△OCF,则可得S四边形AHOF=S△AOC,由平行四边形的性质和直角三角形的性质可求得是AO=OC=2,则可求得答案;
(2)可证得△AEH≌△CGF,则可求得AE=CG,则可求得BG-AH=EF,在Rt△OEF中利用直角三角形的性质可证得结论.
解答 (1)解:
∵AC⊥BC,
∴∠ACB=90°,
∵O为AB中点,
∴OA=OB=OC,OC⊥AB,
∵四边形ABCD为平行四边形,
∴DH∥BC,
∴∠HAO=∠B=45°,
∴∠OCF=∠OAH=45°,
∵OG⊥OE,
∴∠AOH+∠AOG=∠AOG+∠COF,
∴∠AOH=∠COF,
在△OAH和△OCF中
$\left\{\begin{array}{l}{∠OAH=∠OCF}\\{OA=OC}\\{∠AOH=∠COF}\end{array}\right.$
∴△OAH≌△OCF(ASA),
∴S△AOH=S△COF,
∴S四边形AHOF=S△AOF+S△AOH=S△AOF+S△COF=S△AOC,
∵CD=4,
∴AB=4,
∴AO=CO=2,
∴S△AOC=$\frac{1}{2}$OA•OC=$\frac{1}{2}$×2×2=2,
∴S四边形AHOF=2;
(2)证明:
∵△OAH≌△OCF,
∴AH=CF,
∵∠COF=∠AOH=15°,且∠G+∠COF=∠E+∠AOE=45°,
∴∠E=∠G=30°,
在△AHE和△CFG中
$\left\{\begin{array}{l}{∠E=∠G}\\{∠EAH=∠GCF}\\{AH=CF}\end{array}\right.$
∴△AHE≌△CFG(AAS),
∴AE=CG,
∵BC=AC,
∴BG-AH=BG-CF=BC+CG-AH=AC+AE-CF=CE-CF=EF,
在Rt△OEF中,
∵∠E=30°,
∴EF=2OF,
∴BG-AH=2OF.
点评 本题主要考查全等三角形的判定和性质,在(1)中证得△OAH≌△OCF是解题的关键,在(2)中把BG-AH转化成EF是解题的关键,注意直角三角形性质的应用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | k=4 | B. | k>4 | C. | k≤4且k≠0 | D. | k≤4 |
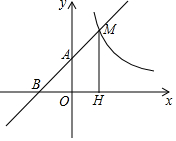 如图,直线y=x+1与x轴交于点B,y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且AO=$\frac{1}{2}$MH.
如图,直线y=x+1与x轴交于点B,y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且AO=$\frac{1}{2}$MH. 如图,已知矩形OABC的面积为50,它的对角线OB与双曲线y=$\frac{k}{x}$相交于点D,且OD:OB=3:5,则k=-18.
如图,已知矩形OABC的面积为50,它的对角线OB与双曲线y=$\frac{k}{x}$相交于点D,且OD:OB=3:5,则k=-18. 如图,是由6个正方体组成的图案,请分别画出从三个方向看到的形状图.
如图,是由6个正方体组成的图案,请分别画出从三个方向看到的形状图.