题目内容
11.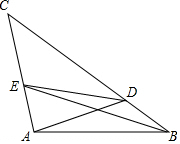 △ABC中,D在BC上,E在AC上,∠BAC=100°,∠ABC=40°,∠BAC=20°,∠ABE=20°,则∠ADE=30°.
△ABC中,D在BC上,E在AC上,∠BAC=100°,∠ABC=40°,∠BAC=20°,∠ABE=20°,则∠ADE=30°.
分析 在BC上截BF=AB,利用全等三角形的判定和性质进行解答即可.
解答 解:在BC上截BF=AB,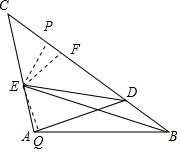
在△ABE与△FBE中
$\left\{\begin{array}{l}{∠ABE=∠FBE=20°}\\{BE=BE}\\{AB=BF}\end{array}\right.$,
∴△ABE≌△FBE(SAS),
∴∠BFE=∠BAE=100°,AE=EF,
∴∠EFP=∠EAD=80°,
过点E作EP⊥BC于点P,EQ⊥AD于点Q,
在Rt△PEF与Rt△QEA中$\left\{\begin{array}{l}{EF=AE}\\{∠EPF=∠EQA=90°}\\{∠PFE=∠EAQ}\end{array}\right.$,
∴Rt△PEF≌Rt△QEA,
∴PE=AE,
∴∠ADE=∠FDE═$\frac{1}{2}×60°=30°$,
故答案为:30°
点评 此题考查三角形内角和问题,关键是根据全等三角形的判定和性质进行解答.

练习册系列答案
相关题目
6.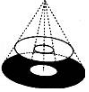 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )| A. | 0.324π m2 | B. | 0.288π m2 | C. | 1.08π m2 | D. | 0.72π m2 |
20.若xmyn÷x3y=x2y,则m、n的值为( )
| A. | m=5,n=0 | B. | m=6,n=0 | C. | m=5,n=2 | D. | m=6,n=2 |

 如图,已知在△ABC中,∠B与∠C的平分线交于点P,∠BPC=125°时,则∠A=70°.
如图,已知在△ABC中,∠B与∠C的平分线交于点P,∠BPC=125°时,则∠A=70°. 如图,在Rt△ABC和Rt△ADE中,AB=AD,AC=AE,∠ACB=∠AED=90°,点C在边AD上,连接BD.
如图,在Rt△ABC和Rt△ADE中,AB=AD,AC=AE,∠ACB=∠AED=90°,点C在边AD上,连接BD.