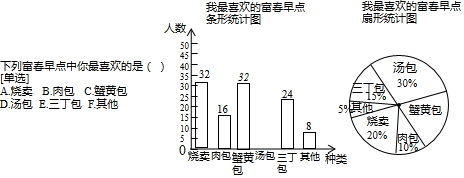
题目内容
17．
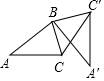如图，将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′，若AB=3，BC=2，则CC′的长为（ ）| A． | 2$\sqrt{2}$ | B． | -2 | C． | 2 | D． | 3 |
分析 根据旋转的性质得到BC′=BC=2，∠CBC′=90°，根据等腰直角三角形的性质即可得到结论．
解答 解：将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′，
∴BC′=BC=2，∠CBC′=90°，
∴CC′=$\sqrt{2}$BC=2$\sqrt{2}$，
故选A．
点评 本题考查了旋转的性质，等腰直角三角形的性质，熟练掌握旋转的性质是解题的关键．
练习册系列答案
相关题目
5．
如图，从与旗杆AB相距27m的点C处，用测角仪CD测得旗杆顶端A的仰角为30°，已知测角仪CD的高为1.5米，则旗杆AB的高约为17.1m（精确到0.1m，参考数据$\sqrt{3}$≈1.73）
如图，从与旗杆AB相距27m的点C处，用测角仪CD测得旗杆顶端A的仰角为30°，已知测角仪CD的高为1.5米，则旗杆AB的高约为17.1m（精确到0.1m，参考数据$\sqrt{3}$≈1.73）
12．
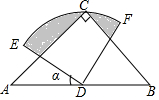如图，在△ABC中，CA=CB，∠ACB=90°，以AB的中点D为圆心，作圆心角为90°的扇形DEF，点C恰在EF上，设∠ADE=α（0°＜α＜90°），当α由小到大变化时，图中阴影部分的面积（ ）
如图，在△ABC中，CA=CB，∠ACB=90°，以AB的中点D为圆心，作圆心角为90°的扇形DEF，点C恰在EF上，设∠ADE=α（0°＜α＜90°），当α由小到大变化时，图中阴影部分的面积（ ）| A． | 由小变大 | B． | 由大变小 | ||
| C． | 不变 | D． | 先由小变大，后由大变小 |
数学活动课，老师和同学一起去测量校内某处的大树AB的高度，如图，老师测得大树前斜坡DE的坡度i=1：4，一学生站在离斜坡顶端E的水平距离DF为8m处的D点，测得大树顶端A的仰角为30°，已知BE=2m，此学生身高CD=1.7m，求大树的高度．（结果保留根号）
已知AB∥CD，AD与BC相交于点O．若$\frac{BO}{OC}$=$\frac{2}{3}$，AD=10，则AO=4．