题目内容
12.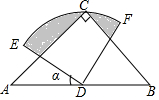 如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠ADE=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠ADE=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )| A. | 由小变大 | B. | 由大变小 | ||
| C. | 不变 | D. | 先由小变大,后由大变小 |
分析 作辅助线,根据直角三角形斜边中线是斜边的一半可知:由于扇形DEF的圆心角为90°,半径为CD,所以扇形DEF的面积为定值,证明∠GDM≌△HDN,则S△GDM=S△HDN,则S四边形CGDH=S正方形CMDN=CM2,则四边形CGDH的面积为定值,所以当α由小到大变化时,图中阴影部分的面积不变.
解答 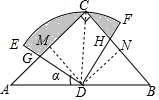 解:连接CD,
解:连接CD,
在△ABC中,CA=CB,∠ACB=90°,
∵D为AB的中点,
∴AD=BD=CD,CD平分∠ACB,
过D作DM⊥AC于M,过D作DN⊥BC于N,
∵CD平分∠ACB,
∴DM=DN,
∵∠DMC=∠ACB=∠DNC=90°,
∴四边形CMDN为正方形,
∴∠MDN=90°,
∵∠EDF=90°,
∴∠GDM=∠NDH,
∴∠GDM≌△HDN,
∴S△GDM=S△HDN,
∴S四边形CGDH=S正方形CMDN=CM2=($\frac{1}{2}$AC)2=$\frac{1}{4}$AC2,
∴四边形CGDH的面积为定值,
∴S阴影=S扇形DEF-S四边形CGDH,
∵扇形DEF的圆心角为90°,半径为CD,
∴扇形DEF的面积为定值,
∴当α由小到大变化时,图中阴影部分的面积不变.
故选C.
点评 本题考查了扇形的面积、等腰直角三角形的性质、正方形的性质和判定、三角形全等的性质和判定,明确利用割补法求不规则图形的面积的方法.

练习册系列答案
相关题目
3.下列说法中正确的是( )
| A. | “任意画出一个等边三角形,它是轴对称图形”是随机事件 | |
| B. | “概率为0.001的事件”是不可能事件 | |
| C. | “任意画出一个平行四边形,它是中心对称图形”是必然事件 | |
| D. | 任意掷一枚质地均匀的硬币10次,正面向上的一定是5次 |
17.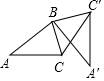 如图,将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′,若AB=3,BC=2,则CC′的长为( )
如图,将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′,若AB=3,BC=2,则CC′的长为( )
 如图,将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′,若AB=3,BC=2,则CC′的长为( )
如图,将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′,若AB=3,BC=2,则CC′的长为( )| A. | 2$\sqrt{2}$ | B. | -2 | C. | 2 | D. | 3 |
4.下列运算中,结果正确的是( )
| A. | (a3)2=a6 | B. | (ab)3=a3b | C. | a•a3=a3 | D. | a8÷a4=a2 |
1.下列各式计算正确的是( )
| A. | (b+2a)(2a-b)=b2-4a2 | B. | 2a3+a3=3a6 | C. | a3•a=a4 | D. | (-a2b)3=a6b3 |
2.中华国山-五岳独尊的泰山,海拔1545米,1545用科学记数法表示为( )
| A. | 1.545×103 | B. | 1.545×104 | C. | 1.545×10-3 | D. | 1.545×10-4 |