题目内容
6.一列数:0,-1,3,-6,10,-15,21,…,按此规律第21个数为210.分析 首先发现奇数位置为正,偶数位置为负;且对应数字依次为0,0+1=1,0+1+2=3,0+1+2+3=6,0+1+2+3+4=0+10,0+1+2+3+4+5=15,0+1+2+3+4+5+6=21,…第n个数字为0+1+2+3+…+(n-1)=$\frac{n(n-1)}{2}$,由此得出答案即可.
解答 解:第n个数字为0+1+2+3+…+(n-1)=$\frac{n(n-1)}{2}$,符号为(-1)n-1,
所以第n个数为(-1)n-1$\frac{n(n-1)}{2}$,
当n=21时,原式=(-1)21-1×$\frac{21×20}{2}$=210.
故答案为:210.
点评 此题考查数字的变化规律,从数的绝对值的和正负情况两个方面考虑求解是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
17.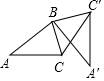 如图,将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′,若AB=3,BC=2,则CC′的长为( )
如图,将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′,若AB=3,BC=2,则CC′的长为( )
 如图,将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′,若AB=3,BC=2,则CC′的长为( )
如图,将△ABC绕点B按逆时针方向旋转90°后得到△A′BC′,若AB=3,BC=2,则CC′的长为( )| A. | 2$\sqrt{2}$ | B. | -2 | C. | 2 | D. | 3 |
14. 如图,在△ABC中,AB=AC,AD平分∠BAC,E为AC的中点,DE=3,则AB等于( )
如图,在△ABC中,AB=AC,AD平分∠BAC,E为AC的中点,DE=3,则AB等于( )
 如图,在△ABC中,AB=AC,AD平分∠BAC,E为AC的中点,DE=3,则AB等于( )
如图,在△ABC中,AB=AC,AD平分∠BAC,E为AC的中点,DE=3,则AB等于( )| A. | 4 | B. | 5 | C. | 5.5 | D. | 6 |
1.下列各式计算正确的是( )
| A. | (b+2a)(2a-b)=b2-4a2 | B. | 2a3+a3=3a6 | C. | a3•a=a4 | D. | (-a2b)3=a6b3 |
15.2的算术平方根是( )
| A. | $±\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 2 |
16.下列运算正确的是( )
| A. | a-(b+c)=a-b+c | B. | 2a2•3a3=6a5 | C. | a3+a3=2a6 | D. | (x+1)2=x2+1 |
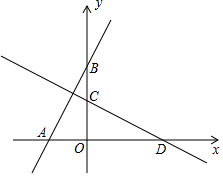 如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.
如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.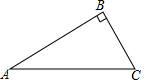 如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2$\sqrt{3}$.
如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2$\sqrt{3}$.