题目内容
6. 已知:如图,△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且CF=DE,求证:∠CDF=∠A.
已知:如图,△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且CF=DE,求证:∠CDF=∠A.
分析 由条件可先证明DE∥CF,结合条件可证明四边形CEDF为平行四边形,可证得∠CDF=∠DCE,再由直角三角形的性质可证得结论.
解答 证明:
∵D、E分别是AC、AB的中点,
∴DE∥BC,
∵点F 在BC的延长线上,
∴DE∥CF,
∵DE=CF,
∴四边形CEDF为平行四边形,
∴DF∥CE,
∴∠CDF=∠ECA,
∵∠ACB=90°,E为AB的中点,
∴CE=$\frac{1}{2}$AB=AE,
∴∠A=∠DCE,
∴∠CDF=∠A.
点评 本题主要考查平行四边形的判定和性质及直角三角形的性质,证明四边形CEDF为平行四边形是解题的关键,注意直线三角形性质的运用.

练习册系列答案
相关题目
16.顺次连结菱形四边中点所得的四边形一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 等腰梯形 |
17.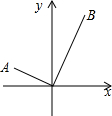 如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
 如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )| A. | 2$\sqrt{5}$ | B. | 4 | C. | $\sqrt{5}$ | D. | 2 |
1.8月份是新学期开学准备季,东风和百惠两书店对学习用品和工具实施优惠销售.优惠方案分别是:在东风书店购买学习用品或工具书累计花费60元后,超出部分按50%收费;在百惠书店购买学习用品或工具书累计花费50元后,超出部分按60%收费,郝爱同学准备买价值300元的学习用品和工具书,她在哪家书店消费更优惠( )
| A. | 东风 | B. | 百惠 | C. | 两家一样 | D. | 不能确定 |
18.等腰△ABC中,已知有一条边长为4,另一条边长为9,则△ABC的周长为( )
| A. | 13 | B. | 17 | C. | 22 | D. | 17或22 |
16.下列各式中,与(1-a)(-a-1)相等的是( )
| A. | a2-1 | B. | a2-2a+1 | C. | a2-2a-1 | D. | a2+1 |

 如图,下列三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.
如图,下列三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.