题目内容
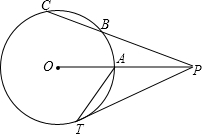 P为以r为半径的⊙O外一点,T是⊙O上一点,PO交⊙O于A点,cos∠OPT=
P为以r为半径的⊙O外一点,T是⊙O上一点,PO交⊙O于A点,cos∠OPT=
| ||
| 2 |
(1)求证:PT是切线;
(2)设PB为x,PC为y求y与x的函数关系式,并指出x的取值范围;
(3)由(2)中,若x、y是关于z的方程4z2-14rz+k=0的两根,且弦长BC=l,求半径r.
考点:圆的综合题
专题:
分析: (1)利用锐角三角函数关系得出∠OPT=30°,进而利用等腰三角形的性质求出∠OTP=90°,进而得出答案;
(1)利用锐角三角函数关系得出∠OPT=30°,进而利用等腰三角形的性质求出∠OTP=90°,进而得出答案;
(2)利用切割线定理得出PT2=PB•PC,进而得出y与x的函数关系式,以及利用等边三角形的性质得出x的取值范围;
(3)利用根据与系数的关系以及(2)中所求得出x、y是方程4z2-14rz+12r2=0的两根,求出x,y的值,进而由BC=1,即可得出答案.
 (1)利用锐角三角函数关系得出∠OPT=30°,进而利用等腰三角形的性质求出∠OTP=90°,进而得出答案;
(1)利用锐角三角函数关系得出∠OPT=30°,进而利用等腰三角形的性质求出∠OTP=90°,进而得出答案;(2)利用切割线定理得出PT2=PB•PC,进而得出y与x的函数关系式,以及利用等边三角形的性质得出x的取值范围;
(3)利用根据与系数的关系以及(2)中所求得出x、y是方程4z2-14rz+12r2=0的两根,求出x,y的值,进而由BC=1,即可得出答案.
解答: (1)证明:连结OT.
(1)证明:连结OT.
∵cos∠OPT=
,
∴∠OPT=30°,
又∵∠OPT=60°,
∴∠ATP=30°,
∵OT=OA,
∴∠OTA=60°,
∴∠OTP=90°,
∴PT是⊙O的切线;
(2)解:∵PT是⊙O的切线,PBC是割线,
∴PT2=PB•PC,
∵PT2=PO2-OT2=(2r)2-r2=3r2,
∴3r2=xy,
故y=
,
∵PA<x=PB≤PT,
由(1)知,△OAT是等边三角形,PA=AT=OA=r,
故自变量x的取值范围为:r≤x<
r;
(3)解:∵x、y是关于z的方程4z2-14rz+k=0的两根,
∴xy=
,由(2)知,
=3r2,则k=12r2,
即x、y是方程4z2-14rz+12r2=0的两根,
解得:x=
r,y=2r或x=2r,y=
r,
由函数自变量的取值范围是:r≤x<
r,而x=2r>
r舍去,
故方程的解是x=
r,y=2r,
∵BC=y-x=2r-
r=
r=1,
解得:r=2.
 (1)证明:连结OT.
(1)证明:连结OT.∵cos∠OPT=
| ||
| 2 |
∴∠OPT=30°,
又∵∠OPT=60°,
∴∠ATP=30°,
∵OT=OA,
∴∠OTA=60°,
∴∠OTP=90°,
∴PT是⊙O的切线;
(2)解:∵PT是⊙O的切线,PBC是割线,
∴PT2=PB•PC,
∵PT2=PO2-OT2=(2r)2-r2=3r2,
∴3r2=xy,
故y=
| 3r2 |
| x |
∵PA<x=PB≤PT,
由(1)知,△OAT是等边三角形,PA=AT=OA=r,
故自变量x的取值范围为:r≤x<
| 3 |
(3)解:∵x、y是关于z的方程4z2-14rz+k=0的两根,
∴xy=
| k |
| 4 |
| k |
| 4 |
即x、y是方程4z2-14rz+12r2=0的两根,
解得:x=
| 3 |
| 2 |
| 3 |
| 2 |
由函数自变量的取值范围是:r≤x<
| 3 |
| 3 |
故方程的解是x=
| 3 |
| 2 |
∵BC=y-x=2r-
| 3 |
| 2 |
| 1 |
| 2 |
解得:r=2.
点评:此题主要考查了圆的综合以及根与系数关系和切割线定理以及锐角三角函数关系等知识,熟练应用切割线定理得出y与x的函数关系是解题关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
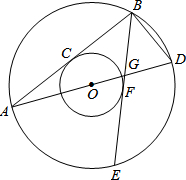 如图,两个同心圆的圆心是O,大圆的半径为10,小圆的半径为6,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
如图,两个同心圆的圆心是O,大圆的半径为10,小圆的半径为6,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.