题目内容
 如图,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q.
如图,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q.当CQ=
| 1 |
| 3 |
当CQ=
| 1 |
| n |
考点:相似三角形的判定与性质
专题:
分析:延长BQ交射线EF于M,根据三角形的中位线平行于第三边可得EF∥BC,根据两直线平行,内错角相等可得∠M=∠CBM,再根据角平分线的定义可得∠PBM=∠CBM,从而得到∠M=∠PBM,根据等角对等边可得BP=PM,求出EP+BP=EM,再根据CQ=
CE求出EQ=2CQ,然后根据△MEQ和△BCQ相似,利用相似三角形对应边成比例列式求解即可.
| 1 |
| 3 |
解答: 解:如图,延长BQ交射线EF于M,
解:如图,延长BQ交射线EF于M,
∵E、F分别是AB、AC的中点,
∴EF∥BC,
∴∠M=∠CBM,
∵BQ是∠CBP的平分线,
∴∠PBM=∠CBM,
∴∠M=∠PBM,
∴BP=PM,
∴EP+BP=EP+PM=EM,
当CQ=
CE时,则EQ=2CQ,
由EF∥BC得,△MEQ∽△BCQ,
∴
=
=2,
∴EM=2BC=2×6=12,
即EP+BP=12;
当CQ=
CE时,则EQ=(n-1)CQ,
由EF∥BC得,△MEQ∽△BCQ,
∴
=
=n-1,
∴EM=(n-1)BC=6(n-1),即EP+BP=6(n-1);
故答案为:12; 6(n-1).
 解:如图,延长BQ交射线EF于M,
解:如图,延长BQ交射线EF于M,∵E、F分别是AB、AC的中点,
∴EF∥BC,
∴∠M=∠CBM,
∵BQ是∠CBP的平分线,
∴∠PBM=∠CBM,
∴∠M=∠PBM,
∴BP=PM,
∴EP+BP=EP+PM=EM,
当CQ=
| 1 |
| 3 |
由EF∥BC得,△MEQ∽△BCQ,
∴
| EM |
| BC |
| EQ |
| CQ |
∴EM=2BC=2×6=12,
即EP+BP=12;
当CQ=
| 1 |
| n |
由EF∥BC得,△MEQ∽△BCQ,
∴
| EM |
| BC |
| EQ |
| CQ |
∴EM=(n-1)BC=6(n-1),即EP+BP=6(n-1);
故答案为:12; 6(n-1).
点评:本题考查了相似三角形的判定与性质,角平分线的定义,平行线的性质,延长BQ构造出相似三角形,求出EP+BP=EM并得到相似三角形是解题的关键,也是本题的难点.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
用配方法解方程x2+2x一5=0时,下列配方结果正确的是( )
| A、(x-1)2=5 |
| B、(x+1)2=6 |
| C、(x+1)2=7 |
| D、(x-1)2=6 |
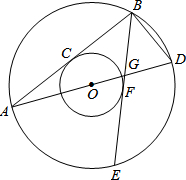 如图,两个同心圆的圆心是O,大圆的半径为10,小圆的半径为6,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
如图,两个同心圆的圆心是O,大圆的半径为10,小圆的半径为6,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD. 如图,⊙O的半径为2,AB、CD是互相垂直的两条直径,点P是⊙O上任意一点,过点P作PM⊥AB于M,PN⊥CD于N,点Q是MN的中点,当点P沿着圆周从D运动到点C时,tan∠QCN的最大值为
如图,⊙O的半径为2,AB、CD是互相垂直的两条直径,点P是⊙O上任意一点,过点P作PM⊥AB于M,PN⊥CD于N,点Q是MN的中点,当点P沿着圆周从D运动到点C时,tan∠QCN的最大值为 如图,在Rt△ABC中,已知∠ACB=90°,AM是BC边的中线,AN是∠BAC的平分线,过点C作CD⊥AN于点D,连接MD,则下列四个结论:
如图,在Rt△ABC中,已知∠ACB=90°,AM是BC边的中线,AN是∠BAC的平分线,过点C作CD⊥AN于点D,连接MD,则下列四个结论: