题目内容
20.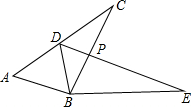 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点F.
如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点F.(1)若∠ABE=160°,∠DBC=30°,求∠CBE的度数;
(2)若AD=DC=3cm,BC=4.5cm,求△DCP与△BPE的周长之和.
分析 (1)根据全等三角形的性质得到∠ABC=∠DBE,计算即可;
(2)根据全等三角形的性质得到BE=BC=4.5cm,DE=AC=6cm,根据三角形的周长公式计算.
解答 解:(1)∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE=$\frac{1}{2}$(160°-30°)=65°;
(2)∵△ABC≌△DBE,
∴BE=BC=4.5cm,DE=AC=6cm,
∴△DCP与△BPE的周长之和=DC+DP+PC+BP+PE+BE=(DP+PE)+(BP+PC)+DC+BE=18cm.
点评 本题考查的是全等三角形的性质,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.

练习册系列答案
相关题目
13.若x-y=3,xy=-1,则代数式2x2y-2xy2的值为( )
| A. | 3 | B. | -3 | C. | -6 | D. | 6 |
14. 如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
下列结论:(1)DE=DF;(2)∠B=∠DGF; (3)AB<AF+FG;(4)若△ABD和△ADG的面积分别是50和38,则△DFG的面积是8.其中一定正确的有( )
 如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.下列结论:(1)DE=DF;(2)∠B=∠DGF; (3)AB<AF+FG;(4)若△ABD和△ADG的面积分别是50和38,则△DFG的面积是8.其中一定正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.2016年全年中国国内生产总值(GDP)约为766000亿元人民币,用科学记数法表示这个数为( )
| A. | 7.66×1012 | B. | 76.6×1012 | C. | 0.766×1013 | D. | 7.66×1013 |
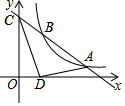 如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(4,n)和点$B(n+\frac{1}{3},3)$,与y轴交于点C.
如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(4,n)和点$B(n+\frac{1}{3},3)$,与y轴交于点C.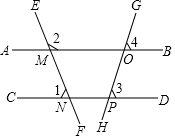 如图,已知∠1=68°,∠3=∠4,求∠2的度数.
如图,已知∠1=68°,∠3=∠4,求∠2的度数.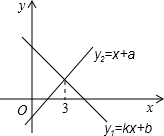 一次函数y1=kx+b与y2=x+a的图象如图所示,则不等式kx+b<x+a的解集为x>3.
一次函数y1=kx+b与y2=x+a的图象如图所示,则不等式kx+b<x+a的解集为x>3.