题目内容
16.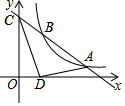 如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(4,n)和点$B(n+\frac{1}{3},3)$,与y轴交于点C.
如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(4,n)和点$B(n+\frac{1}{3},3)$,与y轴交于点C.(1)求反比例函数和一次函数的表达式.
(2)若在x轴上有一点D,其横坐标是1,连接AD、CD,求△ACD的面积.
分析 (1)将点A(4,n)和点$B(n+\frac{1}{3},3)$代入y=$\frac{m}{x}$求得m、n的值,即可得出点A、B的坐标,再利用待定系数法求解可得;
(2)先求得直线y=-$\frac{3}{4}$x+4与x轴交点E的坐标,再根据S△ACD=S△CDE-S△ADE求解得出答案.
解答 解:(1)∵点A(4,n)和点$B(n+\frac{1}{3},3)$均在反比例函数y=$\frac{m}{x}$的图象上,
∴$\left\{\begin{array}{l}{4n=m}\\{3(n+\frac{1}{3})=m}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=4}\\{n=1}\end{array}\right.$,
∴反比例函数的解析式为y=$\frac{4}{x}$,
∴点A(4,1)、B($\frac{4}{3}$,3),
将点A(4,1)、B($\frac{4}{3}$,3)代入y=kx+b,得:
$\left\{\begin{array}{l}{4k+b=1}\\{\frac{4}{3}k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=4}\end{array}\right.$,
∴一次函数的表达式为y=-$\frac{3}{4}$x+4;
(2)设直线y=-$\frac{3}{4}$x+4与x轴交于点E,
则点E的坐标为($\frac{16}{3}$,0),
∴DE=$\frac{16}{3}$-1=$\frac{13}{3}$,
则S△ACD=S△CDE-S△ADE=$\frac{1}{2}$×$\frac{16}{3}$×4-$\frac{1}{2}$×$\frac{13}{3}$×1=$\frac{13}{2}$.
点评 本题考查了用待定系数法求一次函数的解析式和反比例函数的解析式,掌握三角形面积的求法是解题的关键.

 阅读快车系列答案
阅读快车系列答案 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )| A. | ∠1=∠2 | B. | ∠BAD=∠BCD | C. | AO=CO | D. | AC⊥BD |
 已知:如图,四边形ABCD是菱形.以点D为圆心画弧,该弧分别与边AD、CD相交于点E、F,连接BE、BF.求证:BE=BF.
已知:如图,四边形ABCD是菱形.以点D为圆心画弧,该弧分别与边AD、CD相交于点E、F,连接BE、BF.求证:BE=BF.
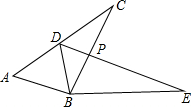 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点F.
如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点F.



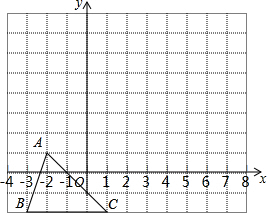 如图,把△ABC向上平移4个的那位长度,再向右平移3个单位长度,得到△A′B′C′.
如图,把△ABC向上平移4个的那位长度,再向右平移3个单位长度,得到△A′B′C′. 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a-2b+c<0;④2a+b<0;⑤4ac-b2<4a;⑥a+b>0中,其中正确的个数为( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a-2b+c<0;④2a+b<0;⑤4ac-b2<4a;⑥a+b>0中,其中正确的个数为( )