题目内容
3.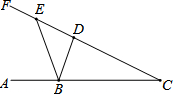 如图,sin∠C=$\frac{3}{5}$,长度为2的线段ED在射线CF上滑动,点B在射线CA上,且BC=5,则△BDE周长的最小值为5+$\sqrt{13}$.
如图,sin∠C=$\frac{3}{5}$,长度为2的线段ED在射线CF上滑动,点B在射线CA上,且BC=5,则△BDE周长的最小值为5+$\sqrt{13}$.
分析 过B作BD⊥CF于D,则此时△BDE的周长最小,解直角三角形得到BE=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,于是得到结论.
解答 解:过B作BD⊥ CF于D,
CF于D,
则此时△BDE的周长最小,
∵sin∠C=$\frac{3}{5}$,BC=5,
∴BD=3,
∵DE=2,
∴BE=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∴△BDE周长的最小值为5+$\sqrt{13}$,
故答案为:5+$\sqrt{13}$.
点评 本题考查了轴对称-最短路线问题,解直角三角形,熟练掌握轴对称的性质是解题的关键.

练习册系列答案
相关题目
13.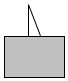 如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )
如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )
 如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )
如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )| A. | 一个锐角 一个钝角 | B. | 两个锐角 | ||
| C. | 一个锐角 一个直角 | D. | 一个直角 一个钝角 |
 如图所示,小明家小区空地上有两棵笔直的树CD、EF.一天,他在A处测得树顶D的仰角∠DAC=32°,在B处测得树顶F的仰角∠FBE=45°,线段BF恰好经过树顶D.已知A、B两处的距离为2米,两棵树之间的距离CE=3米,A、B、C、E四点.在一条直线上,求树EF的高度.(结果精确到0.1米,参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62.)
如图所示,小明家小区空地上有两棵笔直的树CD、EF.一天,他在A处测得树顶D的仰角∠DAC=32°,在B处测得树顶F的仰角∠FBE=45°,线段BF恰好经过树顶D.已知A、B两处的距离为2米,两棵树之间的距离CE=3米,A、B、C、E四点.在一条直线上,求树EF的高度.(结果精确到0.1米,参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62.)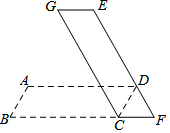 如图,将平行四边形ABCD绕点C顺时针旋转一定角度α(0°<α<180°)后,得到平行四边形EFCG,若BC与CF在同一直线上,且点D恰好在EF上,则α=60°.
如图,将平行四边形ABCD绕点C顺时针旋转一定角度α(0°<α<180°)后,得到平行四边形EFCG,若BC与CF在同一直线上,且点D恰好在EF上,则α=60°. 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形,其中正确结论有①②③④(填序号)
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形,其中正确结论有①②③④(填序号)