题目内容
18．在△ABC中，BC=6，点D、E分别在AB、AC上，DE∥BC，AD=2BD，则DE的长为4．分析 根据相似三角形的判定和性质得到比例式，代入数据即可得到结论．
解答 解：
∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{DE}{BC}=\frac{AD}{AB}$，
∵AD=2BD，
∴$\frac{AD}{AB}=\frac{2}{3}$，
∵BC=6，
∴DE=4，
故答案为：4．
点评 本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，等腰△ABC中，∠CAB=∠CBA，点C、D、E在直线l上，且∠ADC=∠ACB=∠BEC．
6．一元二次方程3x（x+1）=3x+3的解为（ ）
| A． | x=1 | B． | x=-1 | C． | x1=1，x2=-1 | D． | x1=0，x2=-1 |
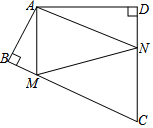如图，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，AB=1，AD=2，在BC、CD上分别找一点M、N，使△AMN周长最小，则最小值为2$\sqrt{7}$．
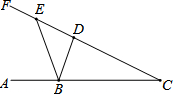如图，sin∠C=$\frac{3}{5}$，长度为2的线段ED在射线CF上滑动，点B在射线CA上，且BC=5，则△BDE周长的最小值为5+$\sqrt{13}$．
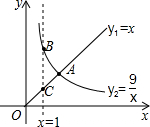函数y1=x（x≥0），y2=$\frac{9}{x}$（x＞0）的图象如图所示，则结论：