题目内容
8.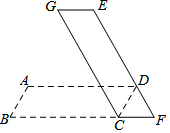 如图,将平行四边形ABCD绕点C顺时针旋转一定角度α(0°<α<180°)后,得到平行四边形EFCG,若BC与CF在同一直线上,且点D恰好在EF上,则α=60°.
如图,将平行四边形ABCD绕点C顺时针旋转一定角度α(0°<α<180°)后,得到平行四边形EFCG,若BC与CF在同一直线上,且点D恰好在EF上,则α=60°.
分析 由旋转的性质得出CD=CF,得出∠CDF=∠F,由平行四边形的性质得出∠ADC=∠DCF,证出∠CDF=∠F=∠DCF,得出∠DCF=60°即可.
解答 解:由旋转的性质得:CD=CF,
∴∠CDF=∠F,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AD∥BF,
∴∠ADC=∠DCF,
又∵∠ADC=∠F,
∴∠CDF=∠F=∠DCF,
∴∠DCF=60°,
即旋转的角度α=60°,
故答案为:60°.
点评 本题考查了旋转的性质、平行四边形的性质;熟练掌握平行四边形的性质和旋转的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
16.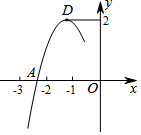 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,其中错误的结论为( )
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,其中错误的结论为( )
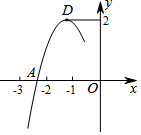 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,其中错误的结论为( )
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,其中错误的结论为( )| A. | 方程ax2+bx+c=0的根为-1 | B. | b2-4ac>0 | ||
| C. | a=c-2 | D. | a+b+c<0 |
17. 如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形边长为( )
如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形边长为( )
 如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形边长为( )
如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=3,则小正方形边长为( )| A. | 6 | B. | 5 | C. | $\frac{15}{4}$ | D. | $\sqrt{12}$ |
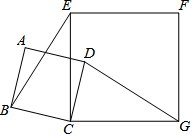 如图,在正方形ABCD和正方形ECGF中,连接BE,DG.求证:BE=DG.
如图,在正方形ABCD和正方形ECGF中,连接BE,DG.求证:BE=DG.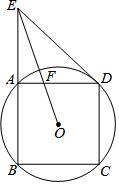 如图,正方形ABCD接于⊙O,延长BA到E,使AE=AB,连接ED.
如图,正方形ABCD接于⊙O,延长BA到E,使AE=AB,连接ED.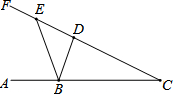 如图,sin∠C=$\frac{3}{5}$,长度为2的线段ED在射线CF上滑动,点B在射线CA上,且BC=5,则△BDE周长的最小值为5+$\sqrt{13}$.
如图,sin∠C=$\frac{3}{5}$,长度为2的线段ED在射线CF上滑动,点B在射线CA上,且BC=5,则△BDE周长的最小值为5+$\sqrt{13}$. 如图,⊙O是△ABC的外接圆,OD⊥弦BC,垂足为D,若∠O=50°,则∠A=130°.
如图,⊙O是△ABC的外接圆,OD⊥弦BC,垂足为D,若∠O=50°,则∠A=130°. 解方程:
解方程: