题目内容
15.甲乙两名同学做摸牌游戏.他们在桌上放了一副扑克牌中的4张牌,牌面分别是J,Q,K,K.将牌面全部朝下.(1)若随机从中抽出一张牌,牌面是K的概率为$\frac{1}{2}$
(2)若从这4张牌中随机取1张牌记下结果放回,洗匀后再随机取1张牌,若两次取出的牌中都没有K,则甲获胜,否则乙获胜.你认为甲乙两人谁获胜的可能性大?用列表或画树状图的方法说明理由.
分析 (1)随机从中抽出一张牌,一共有四种可能,牌面是K的有两种可能,由此可知随机从中抽出一张牌牌面是K的概率=$\frac{1}{2}$.
(2)分别求出甲获胜与乙获胜的概率,进行比较,即可得出结论.
解答 解:(1)∵随机从中抽出一张牌,一共有四种可能,牌面是K的有两种可能,
∴随机从中抽出一张牌,牌面是K的概率=$\frac{2}{4}$=$\frac{1}{2}$.
故答案为$\frac{1}{2}$
(2)乙获胜的可能性大.理由如下,
进行一次游戏所有可能出现的结果如下表:
从上表可以看出,一次游戏可能出现的结果共有16种,而且每种结果出现的可能性相等,其中两次取出的牌中都没有K的有(J,J),(J,Q),(Q,J),(Q,Q)等4种结果.
∵P(两次取出的牌中都没有K)=$\frac{4}{16}$.
∴P(甲获胜)=$\frac{1}{4}$,P(乙获胜)=$\frac{3}{4}$.
∵$\frac{1}{4}$<$\frac{3}{4}$,
∴乙获胜的可能性大.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
6.一元二次方程3x(x+1)=3x+3的解为( )
| A. | x=1 | B. | x=-1 | C. | x1=1,x2=-1 | D. | x1=0,x2=-1 |
10.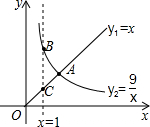 函数y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的图象如图所示,则结论:
函数y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的图象如图所示,则结论:
①两函数图象的交点A的坐标为(3,3 );
②当x<3时,y2>y1;
③当x=1时,BC=8;
④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是( )
 函数y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的图象如图所示,则结论:
函数y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的图象如图所示,则结论:①两函数图象的交点A的坐标为(3,3 );
②当x<3时,y2>y1;
③当x=1时,BC=8;
④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是( )
| A. | ①③④ | B. | ①②③④ | C. | ②③④ | D. | ①③ |
4.若a2=(-3)2,那么a等于( )
| A. | -3 | B. | 3 | C. | 9 | D. | 3或-3 |
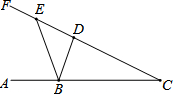 如图,sin∠C=$\frac{3}{5}$,长度为2的线段ED在射线CF上滑动,点B在射线CA上,且BC=5,则△BDE周长的最小值为5+$\sqrt{13}$.
如图,sin∠C=$\frac{3}{5}$,长度为2的线段ED在射线CF上滑动,点B在射线CA上,且BC=5,则△BDE周长的最小值为5+$\sqrt{13}$. 将如图所示的长方形绕图中的虚线旋转360°得到的几何体是( )
将如图所示的长方形绕图中的虚线旋转360°得到的几何体是( )


