题目内容
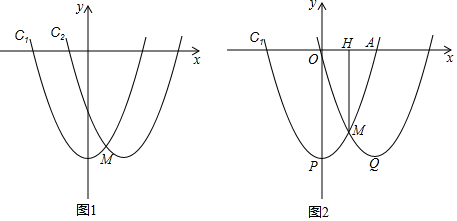
12.在平面直角坐标系xOy中,把抛物线C1:y=x2-4沿x轴向右平移m(m>0)个单位长度,得抛物线C2,C1和C2的交点为点M(如图1)(1)用含m的式子来表示抛物线C2的解析式和点M的坐标;
(2)定义:像C1和C2两条抛物线,是把其中一条沿水平方向向左(像向右)平移得到另一条.若两抛物线的顶点P、Q以及交点M满足∠PMQ=90°,则这样的两条抛物线互为“和谐线”.
①求抛物线C1:y=x2-4的和谐线;
②如图2,抛物线C1:y=x2-4与x轴正半轴的交点为A,与它的和谐线的交点为M(点M在第四象限),连接MA,过点M作MH⊥x轴,在x轴上存在一点N,使∠ONM+∠AMH=45°,求点N的坐标
分析 (1)利用平移的性质即可得出结论,再联立方程组求解即可得点M的坐标;
(2)由和谐线的意义得出△PMQ是等腰直角三角形,利用等腰直角三角形的性质即可得出m的值,
(3)先确定出直线OM的解析式,进而求出过原点而垂直于OM的直线的解析式,利用OD=OM求出点D的坐标,即可得出直线DM的解析式,与x轴的交点是点N即可,同理得出x轴正半轴上的一个点.
解答 解:(1)∵抛物线C1:y=x2-4①沿x轴向右平移m(m>0)个单位长度,得抛物线C2,
∴抛物线C2的解析式为y=(x-m)2-4=x2-2mx+m2-4②,
联立①②得,x=$\frac{m}{2}$,y=$\frac{{m}^{2}}{4}$-4,
∴M($\frac{m}{2}$,$\frac{{m}^{2}}{4}-4$);
(2)设抛物线C1:y=x2-4的和谐线抛物线C2的解析式为y=(x-m)2-4,
∴抛物线C1的顶点P(0,-4),抛物线C2的顶点Q(m,-4),
∴PQ=|m|,同(1)的方法得,M($\frac{m}{2}$,$\frac{{m}^{2}}{4}-4$);
由“和谐线”的定义,易知,△PMQ是等腰直角三角形,
∴$\frac{{m}^{2}}{4}$-4+4=$\frac{1}{2}$|m|,
∴m=-2或m=2,
∴抛物线C2的解析式为y=(x-2)2-4或y=(x+2)2-4.
(3)当点N在x轴负半轴上时,如图,
由(2)知,M(1,-3),抛物线C2过原点,
∴直线OM的解析式为y=-3x,
过点O作OD⊥OM,截取OD=OM,
∴△ODM是等腰直角三角形,
∴∠ODM=45°,
∵∠DON+∠MOA=90°,∠OMH+∠MOH=90°,
∴∠DON=∠OMH,
∵∠OMH=∠AMH,
∴∠AMH=∠DON,
∴直线OD的解析式为y=$\frac{1}{3}$x,
设点D的坐标为(3m,m)(m<0),
∴9m2+m2=10,
∴m=1(舍)或m=-1,
∴D(-3,-1),
∵M(1,-3),
∴直线DM的解析式为y=-$\frac{1}{2}$x-$\frac{5}{2}$,
令y=0,得-$\frac{1}{2}$x-$\frac{5}{2}$=0,
∴x=-5,
∴N(-5,0),
同理可得,x轴正半轴上的一个N点的坐标为(7,0).
即:满足条件的点N(-5,0)或(7,0).
点评 此题是二次函数综合题,主要考查了平移的性质,和谐线的意义的理解和应用,和谐线的特点,解(2)的关键是利用等腰直角三角形的性质建立方程,解(3)的关键是找出点N的位置,是一道典型的新定义题目.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案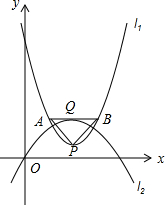 定义:若两条抛物线的对称轴相同则称这两条抛物线为同轴抛物线.
定义:若两条抛物线的对称轴相同则称这两条抛物线为同轴抛物线.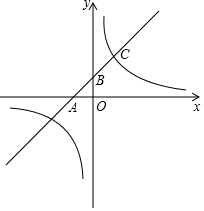 已知:如图,一次函数y=kx+b的图象与x轴负半轴相交于点A,与y正半轴相交于点B,与反比例函数y=$\frac{m}{x}$图象的一个交点为C(2,4),且 AB=BC.
已知:如图,一次函数y=kx+b的图象与x轴负半轴相交于点A,与y正半轴相交于点B,与反比例函数y=$\frac{m}{x}$图象的一个交点为C(2,4),且 AB=BC.
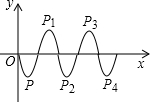 如图,将顶点为P(1,-2),且过原点的抛物线y的一部分沿x轴翻折并向右平移2个单位长度,得到抛物线y1,其顶点为P1,然后将抛物线y1沿x轴翻折并向右平移2个单位长度,得到抛物线y2,其顶点为P2;…,如此进行下去,直至得到抛物线y2016,则点P2016坐标为(4033,-2).
如图,将顶点为P(1,-2),且过原点的抛物线y的一部分沿x轴翻折并向右平移2个单位长度,得到抛物线y1,其顶点为P1,然后将抛物线y1沿x轴翻折并向右平移2个单位长度,得到抛物线y2,其顶点为P2;…,如此进行下去,直至得到抛物线y2016,则点P2016坐标为(4033,-2).