Question

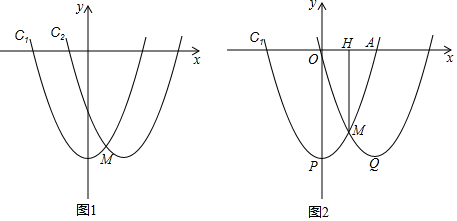
2．在△ABC中，∠ABC=45°，AB=2$\sqrt{2}$，线段AB的垂直平分线交直线BC于点E，若CE=1，则BC边的长为3或1．

Answer 1

分析 分两种情况：如图1，如图2，根据线段垂直平分线的性质和等腰直角三角形的性质即可得到结论．

解答 解：如图1，∵线段AB的垂直平分线交直线BC于点E，
∵∠ABC=45°，AB=2$\sqrt{2}$，
∴BD=$\sqrt{2}$，
∴BE=$\sqrt{2}$BD=2，
∵CE=1，
∴BC=3；
如图2，∵线段AB的垂直平分线交直线BC于点E，
∵∠ABC=45°，AB=2$\sqrt{2}$，
∴BE=2，
∵CE=1，
∴BC=1，
综上所述，BC=3或1．
故答案为：3或1．

点评 本题考查了线段垂直平分线的性质，等腰直角三角形的性质，正确的作出图形是解题的关键．