题目内容
4. 如图,△ABC中,∠ABC=40°,BD平分∠ABC,BC=BD+AD.求证:AB=AC.
如图,△ABC中,∠ABC=40°,BD平分∠ABC,BC=BD+AD.求证:AB=AC.
分析 在BC上取一点E,是BE=BD,作DF⊥BA于F,DG⊥BC于G,由角平分线的性质就可以得出DF=DG,进而可以得出△DAF≌△DEG,就有DA=DE,再由求出DE=CE就可以得出结论.
解答 解:在BC上取一点E,是BE=BD,作DF⊥BA于F,DG⊥BC于G,
∴∠DFA=∠DGE=90°.
∵BD平分∠ABC,DF⊥BA,DG⊥BC,
∴DF=DG.
∵∠ABC=40°,
∴∠ABD=∠DBE=20°,
∴∠BDF=70°,
∵BE=BD,∠DBC=20°,
∴∠BED=∠BDE=80°,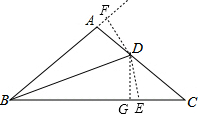
∴∠BDF=∠BED,
在△DAF和△DEG中,
$\left\{\begin{array}{l}{∠DFA=∠DGE}\\{∠BAC=∠BED}\\{DF=DG}\end{array}\right.$,
∴△DAF≌△DEG(AAS),
∴AD=ED,
∵BC=BD+AD,
∴BC=BD+DE=BE+CE,
∴DE=CE,
∵∠BED=∠C+∠EDC,
∴80°=∠C+∠EDC,
∴∠C=40°,
∴∠ABC=∠C,
∴AB=AC.
点评 本题考查了等腰三角形的性质的运用,角平分线的性质的运用,全等三角形的判定及性质的运用,解答时合理添加辅助线是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.函数y=$\frac{1}{{x}^{2}+ax+b}$(a,b为非0常数)取得最大值的条件是( )
| A. | a2-4b≥0 | B. | a2-4b≠0 | ||
| C. | a2-4b<0 | D. | 与a,b取值有关,不能确定 |
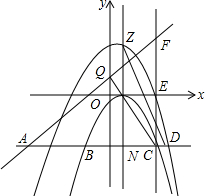 如图,已知过点(0,-$\frac{1}{4}$)的抛物线C1:y=ax2+bx+c的顶点为Q(1,0),现将该抛物线上所有点的纵坐标加h(h>0),横坐标不变,得到新的抛物线,记为C2,在y轴的负半轴作一条平行于x轴的直线,与两条抛物线交于A、B、C、D四点,直线AD与x轴的距离是m2(m>0)
如图,已知过点(0,-$\frac{1}{4}$)的抛物线C1:y=ax2+bx+c的顶点为Q(1,0),现将该抛物线上所有点的纵坐标加h(h>0),横坐标不变,得到新的抛物线,记为C2,在y轴的负半轴作一条平行于x轴的直线,与两条抛物线交于A、B、C、D四点,直线AD与x轴的距离是m2(m>0)
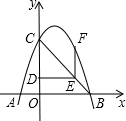 如图所示,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.
如图所示,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.