题目内容
11.如图,依次连接一个边长为1的正方形各边的中点,得到第二个正方形,再依次连接第二个正方形各边的中点,得到第三个正方形,按此方法继续下去,则第2016个正方形的面积是$\frac{1}{{2}^{2015}}$.
分析 分割图形,会发现每经过一次操作面积减半,结合第一个图形的面积即可得出结论.
解答 解:按下面图形所示对正方形进行分割,
由分割原理可知,每分一次面积减少一倍.
∵第一个正方形的面积为1×1=1,
∴第2016个正方形的面积是$\frac{1}{{2}^{2016-1}}$.
故答案为$\frac{1}{{2}^{2015}}$.
点评 本题考查了图形的变化,解题的关键是通过分割图形找出变化规律.本题属于基础题,难度不大,解决该题型题目时,通过图形的变化找出规律是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.一组数据3,3,2,5,8,8的中位数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 8. |
2.九年级一班数学老师对全班学生在模拟考试中A卷成绩进行统计后,制成如下的统计表:
则该班学生A卷成绩的众数和中位数分别是( )
| 成绩(分) | 80 | 82 | 84 | 86 | 87 | 90 |
| 人数 | 8 | 12 | 9 | 3 | 5 | 8 |
| A. | 82分,82分 | B. | 82分,83分 | C. | 80分,82分 | D. | 82分,84分 |
19.当前,雾霾严重.治理雾霾方法之一是将已生产的PM2.5吸纳降解.研究表明:雾霾的程度随城市中心区立体绿化面积的增大而减小,在这个问题中,自变量是( )
| A. | 城市中心立体绿化面积 | B. | PM2.5 | ||
| C. | 雾霾 | D. | 雾霾程度 |
20.函数y=$\frac{1}{{x}^{2}+ax+b}$(a,b为非0常数)取得最大值的条件是( )
| A. | a2-4b≥0 | B. | a2-4b≠0 | ||
| C. | a2-4b<0 | D. | 与a,b取值有关,不能确定 |
20.下列图形中,既是轴对称图形,又是中心对称图形是( )
| A. |  | B. |  | C. |  | D. |  |
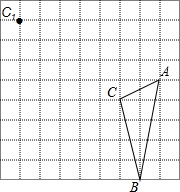 在边长为1的正方形网格中有△ABC,将这个三角形进行平移,使C点的对称点C1,
在边长为1的正方形网格中有△ABC,将这个三角形进行平移,使C点的对称点C1,