题目内容
9. 如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )
如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
分析 设∠ABD=∠CBD=x°,则∠ABC=2x°,根据线段垂直平分线性质求出BF=CF,推出∠FCB=∠CBD,根据三角形内角和定理得出方程,求出方程的解即可.
解答 解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
设∠ABD=∠CBD=x°,则∠ABC=2x°,
∵EF是BC的垂直平分线,
∴BF=CF,
∴∠FCB=∠CBD=x°,
∵∠A=60°,∠ACF=45°,
∴60°+45°+x°+2x°=180°,
解得:x=25,
∴∠ABC=2x°=50°,
故选B.
点评 本题考查了三角形内角和定理,线段垂直平分线性质的应用,能求出BF=CF是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列调查适合作普查的是( )
| A. | 了解“嫦娥三号”卫星零部件的状况 | |
| B. | 了解在校大学生的主要娱乐方式 | |
| C. | 日光灯管厂要检测一批灯管的使用寿命 | |
| D. | 了解某市居民对废电池的处理情况 |
19.化简$\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$-$\frac{b}{a+b}$的结果是( )
| A. | $\frac{a}{a-b}$ | B. | $\frac{b}{a-b}$ | ||
| C. | $\frac{{a}^{2}+ab+2{b}^{2}}{{a}^{2}-{b}^{2}}$ | D. | $\frac{{a}^{2}+ab+{b}^{2}}{{a}^{2}-{b}^{2}}$ |
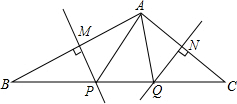 如图,在△ABC的边AB和AC的垂直平分线分别交BC于P、Q,若∠BAC=100°,则∠PAQ=20;若∠BAC+∠PAQ=150°,则∠PAQ=40°.
如图,在△ABC的边AB和AC的垂直平分线分别交BC于P、Q,若∠BAC=100°,则∠PAQ=20;若∠BAC+∠PAQ=150°,则∠PAQ=40°.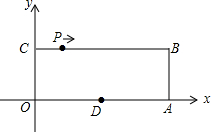 如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.