题目内容
19.化简$\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$-$\frac{b}{a+b}$的结果是( )| A. | $\frac{a}{a-b}$ | B. | $\frac{b}{a-b}$ | ||
| C. | $\frac{{a}^{2}+ab+2{b}^{2}}{{a}^{2}-{b}^{2}}$ | D. | $\frac{{a}^{2}+ab+{b}^{2}}{{a}^{2}-{b}^{2}}$ |
分析 先将分母因式分解以确定最简公分母为(a+b)(a-b),再通分化为同分母分式,依据分式加减法则运算即可.
解答 解:$\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$-$\frac{b}{a+b}$=$\frac{{a}^{2}+2ab+{b}^{2}}{(a+b)(a-b)}$-$\frac{b(a-b)}{(a+b)(a-b)}$
=$\frac{{a}^{2}+2ab+{b}^{2}-ab+{b}^{2}}{(a+b)(a-b)}$
=$\frac{{a}^{2}+ab+2{b}^{2}}{{a}^{2}-{b}^{2}}$,
故选:C.
点评 本题主要考查分式的加减运算,异分母分式相加减,先通分,变为同分母分式,再利用同分母分式的加减法则计算.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
9. 如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )
如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )
 如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )
如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF=45°,则∠ABC的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
10.(-$\frac{1}{3}$)-1-4cos30°+|-$\sqrt{12}$|的计算结果为( )
| A. | -4 | B. | 4 | C. | -3 | D. | -2 |
19.小莹用描点法画二次函数y=ax2+bx+c时,列出了下表:
(1)你能根据表格中的信息,求出该二次函数当x=3时,y的值吗?
(2)试从表中选择适当的数据,求出该二次函数的表达式.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{3}{16}$ | -4 | -$\frac{5}{2}$ | -2 | -$\frac{5}{2}$ | … |
(2)试从表中选择适当的数据,求出该二次函数的表达式.
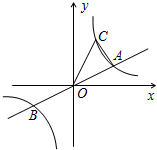 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=$\frac{k}{x}$上一点,且点C在直线y=$\frac{1}{2}$x的上方.
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=$\frac{k}{x}$上一点,且点C在直线y=$\frac{1}{2}$x的上方.