题目内容
14.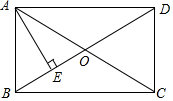 如图,矩形ABCD中,对角线AC、BD相交于点O,且AC=8,AE垂直平分OB于点E,则矩形ABCD的面积为16$\sqrt{3}$.
如图,矩形ABCD中,对角线AC、BD相交于点O,且AC=8,AE垂直平分OB于点E,则矩形ABCD的面积为16$\sqrt{3}$.
分析 根据矩形的性质判断出OA=OB,由线段垂直平分线的性质得出AB=OA=4,由勾股定理求出BC,即可得出矩形的面积.
解答 解:∵四边形ABCD是矩形,
∴∠ABC=90°,AO=OC=$\frac{1}{2}$AC=4,
∵AE垂直平分OB,
∴AB=AO=4,
由勾股定理得:BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$;
∴矩形ABCD的面积=AB×BC=4×4$\sqrt{3}$=16$\sqrt{3}$.
故答案为16$\sqrt{3}$.
点评 本题考查了矩形的性质、线段垂直平分线的性质、勾股定理以及矩形面积的计算;熟练掌握矩形的性质,由勾股定理求出BC是解决问题的关键.

练习册系列答案
相关题目
4.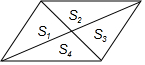 如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )
如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )
 如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )
如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )| A. | S1<S2<S3<S4 | B. | S1=S2=S3=S4 | C. | S1+S2>S3+S4 | D. | S1=S3<S2=S4 |
9.下列二次根式,化简后能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{0.3}$ | D. | $\sqrt{18}$ |
3.若一个多边形的每个内角都为108°,则它的边数为( )
| A. | 5 | B. | 8 | C. | 6 | D. | 10 |
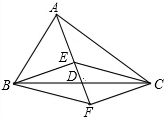 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是②(只填写序号).
如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是②(只填写序号).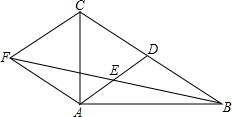 如图,在△ABC中,AD是边BC上的中线,E是AD的中点,过点A作BC的平行线AF交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是边BC上的中线,E是AD的中点,过点A作BC的平行线AF交BE的延长线于点F,连接CF.