题目内容
8.若x2+x-5=0,则代数式x3+6x2+3的值为28.分析 由x2+x-5=0,得出x2+x=5,进一步把代数式x3+6x2+3变形整体代入求得结果即可.
解答 解:∵x2+x-5=0,
∴x2+x=5,
∴x3+6x2+3
=x(x2+x)+5x2+3
=5(x2+x)+3
=25+3
=28.
故答案为:28.
点评 此题考查代数式求值,以及因式分解的运用,注意式子的特点,灵活变形解决问题.

练习册系列答案
相关题目
1.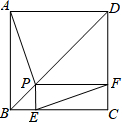 如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为$\sqrt{2}$;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为$\sqrt{2}$;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
 如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为$\sqrt{2}$;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为$\sqrt{2}$;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
19.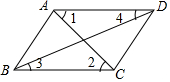 如图,下列条件中,不能判定AD∥BC的是( )
如图,下列条件中,不能判定AD∥BC的是( )
 如图,下列条件中,不能判定AD∥BC的是( )
如图,下列条件中,不能判定AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠ADC+∠DCB=180° | D. | ∠BAD+∠ADC=180° |
20.已知a、b、c是△ABC的三边长,且|a-3|+(4-b)2+$\sqrt{c-5}$=0,则△ABC是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 等腰直角三角形 | D. | 直角三角形 |
17.如果△ABC三边a、b、c满足(a-4)2+$\sqrt{b-3}$+|c-5|=0,那么△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 直角三角形 |
18.下列说法正确的是( )
| A. | 投掷质量分布均匀的六面体骰子600次,骰子六面分别标有1,2,3,4,5,6,那么出现5点的机会大约为100次 | |
| B. | 抛掷硬币实验中,抛掷500次和抛掷1000次没什么区别 | |
| C. | 现有9张卡片,分别标有1至9这九个数字,将它们背面朝上洗匀后,任意抽出一张,因小丽的幸运数是“8”,所以她抽到数字8的机会比抽到其他数字的机会大 | |
| D. | 某彩票的中奖机会是1%,买1张一定不会中奖 |
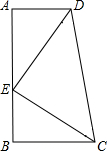 如图,在梯形ABCD中,AD∥BC,∠A=90°,点E在边AB上,AD=BE,AE=BC,由此可以知道△ADE旋转后能与△BEC重合,那么旋转中心是CD的中点.
如图,在梯形ABCD中,AD∥BC,∠A=90°,点E在边AB上,AD=BE,AE=BC,由此可以知道△ADE旋转后能与△BEC重合,那么旋转中心是CD的中点.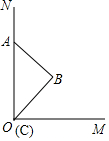 已知OM⊥ON,斜边长为4的等腰直角△ABC的斜边AC在射线上,顶点C与O重合,若点A沿NO方向向O运动,△ABC的顶点C随之沿OM方向运动,点A移动到点O为止,则直角顶点B运动的路径长是8-4$\sqrt{2}$.
已知OM⊥ON,斜边长为4的等腰直角△ABC的斜边AC在射线上,顶点C与O重合,若点A沿NO方向向O运动,△ABC的顶点C随之沿OM方向运动,点A移动到点O为止,则直角顶点B运动的路径长是8-4$\sqrt{2}$.