已知a.b.c是△ABC的三边长.且|a-3|+(4-b)2+$\sqrt{c-5}$=0.则△ABC是( )A．等腰三角形B．等边三角形C．等腰直角三角形D．直角三角形题目和参考答案——青夏教育精英家教网—

题目内容

20．已知a、b、c是△ABC的三边长，且|a-3|+（4-b）²+$\sqrt{c-5}$=0，则△ABC是（　　）

A．

等腰三角形

B．

等边三角形

C．

等腰直角三角形

D．

直角三角形

分析先求出a、b、c的值，根据勾股定理的逆定理求出△ABC是直角三角形，即可得出选项．

解答解：∵|a-3|+（4-b）²+$\sqrt{c-5}$=0，
∴a-3=0，4-b=0，c-5=0，
∴a=3，b=4，c=5，
∴a²+b²=c²，
∴△ABC是直角三角形，
故选D．

点评本题考查了勾股定理的逆定理，绝对值、偶次方、算术平方根的非负性等知识点，能熟记勾股定理的逆定理的内容是解此题的关键．

练习册系列答案

大爱图书纵向解析与命题设计中考试题精选系列答案

11．已知多项式A=-a²b-2（2ab²-a²b），另一个多项式B，其与A的和为-ab²，解答下面的问题：
（1）求多项式B；
（2）若（a-1）²+$\sqrt{b+2}$=0，求A-2B的值．

8．若x²+x-5=0，则代数式x³+6x²+3的值为28．

15．

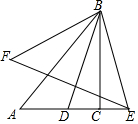如图，在Rt△BAC中，∠ACB=Rt∠，AC=6，BC=8，D是AC边上的一点，点D关于BC的对称点为E，关于AB的对称点为F，连接BD，BE，BF，EF，若BD平分∠ABC，则EF的长为$\frac{16}{5}\sqrt{10}$．

5．

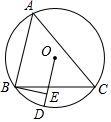如图．边长为2$\sqrt{3}$的等边△ABC内接于圆O．D为弧BC上一点、过点B作BE⊥OD于点E，当点D从B点沿弧BC运动到点C时．点E经过的路径长为$\frac{4}{3}$π（结果保留π）．

12．

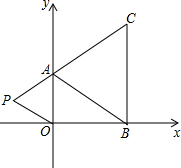在如图直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a，b，c满足关系$\sqrt{a-2}+（b-3）^{2}$=0，（c-4）²≤0，点P、点A、点C在同一条直线上．
（1）求a、b、c的值；
（2）如果点P（m，n）在第二象限，四边形CBOP的面积为y，请你用含m，n的式子表示y；并求出m，n之间的关系；
（3）在满足（2）的条件下，若PE∥OB交AB于点E，PO∥AB，求点E，点P的坐标．

9．已知方程|x-a|+|x+a|=a有解，那么有理数a的值是（　　）

10．如图图形中，是轴对称图形的有（　　）

试题分类