题目内容
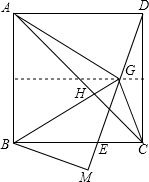 在正方形ABCD中,点E为BC边上的一点,连接DE,点G为DE中点,连接GA、GB、GC,GB与AC交于点H,过点B作BM⊥DE延长线于点M.求证:GA=GB.
在正方形ABCD中,点E为BC边上的一点,连接DE,点G为DE中点,连接GA、GB、GC,GB与AC交于点H,过点B作BM⊥DE延长线于点M.求证:GA=GB.考点:正方形的性质,全等三角形的判定与性质
专题:证明题
分析:根据正方形的性质求得AD=BC,∠BCD=90°,然后根据直角三角形斜边上中线的性质求得CG=GE=GD,∠GCD=∠GDC,根据等量减等量求得∠BCG=∠ADG,根据SAS求得△ADG≌△BCG,从而证得GA=GB.
解答:证明:∵正方形ABCD,
∴AD=BC,∠BCD=90°,
又∵点G为DE中点,
∴CG=GE=GD,
∴∠GCD=∠GDC,
∴∠BCG=∠ADG,
在△ADG与△BCG中,
,
∴△ADG≌△BCG(SAS),
∴GA=GB.
∴AD=BC,∠BCD=90°,
又∵点G为DE中点,
∴CG=GE=GD,
∴∠GCD=∠GDC,
∴∠BCG=∠ADG,
在△ADG与△BCG中,
|
∴△ADG≌△BCG(SAS),
∴GA=GB.
点评:本题考查了正方形的性质,直角三角形中线的性质,三角形全等的判定和性质,根据直角三角形中线的性质求得CG=GE=GD,∠GCD=∠GDC,是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,若AB∥EF,用含α、β、γ的式子表示x,应为( )
如图,若AB∥EF,用含α、β、γ的式子表示x,应为( )| A、α+β+γ |
| B、β+γ-α |
| C、180°-α-γ+β |
| D、180°+α+γ+β |
若点(t,t)在函数y=ax2+bx+c的图象上,则称点(t,t)为函数y=ax2+bx+c的不动点,若二次函数y=ax2-3x+b有两个不动点,则下列结论正确的是( )
| A、ab<4 | B、ab=4 |
| C、ab>4 | D、ab≤4 |
 画出下列几何体的三视图.
画出下列几何体的三视图.