题目内容
观察下列各式的计算结果
1-
=1-
=
=
×
1-
=1-
=
=
×
1-
=1-
=
=
×
1-
=1-
=
=
×
(1)用你发现的规律填写下列式子的结果:
1-
= × ;1-
= × ;1-
= ×
(2)用你发现的规律计算:
(1-
)×(1-
)×(1-
)×…×(1-
)×(1-
)
1-
| 1 |
| 22 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
1-
| 1 |
| 32 |
| 1 |
| 9 |
| 8 |
| 9 |
| 2 |
| 3 |
| 4 |
| 3 |
1-
| 1 |
| 42 |
| 1 |
| 16 |
| 15 |
| 16 |
| 3 |
| 4 |
| 5 |
| 4 |
1-
| 1 |
| 52 |
| 1 |
| 25 |
| 24 |
| 25 |
| 4 |
| 5 |
| 6 |
| 5 |
(1)用你发现的规律填写下列式子的结果:
1-
| 1 |
| 102 |
| 1 |
| 1002 |
| 1 |
| 20122 |
(2)用你发现的规律计算:
(1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 20112 |
| 1 |
| 20122 |
考点:有理数的混合运算
专题:
分析:(1)原式各项利用平方差公式变形,即可得到结果;
(2)利用得出的规律变形,计算即可得到结果.
(2)利用得出的规律变形,计算即可得到结果.
解答:解:(1)1-
=
×
;1-
=
×
;1-
=
×
;
(2)根据题意得:原式=
×
×
×
×…×
×
×
=
×
=
.
故答案为:(1)
;
;
;
;
;
| 1 |
| 102 |
| 9 |
| 10 |
| 11 |
| 10 |
| 1 |
| 1002 |
| 99 |
| 100 |
| 101 |
| 100 |
| 1 |
| 20122 |
| 2011 |
| 2012 |
| 2013 |
| 2012 |
(2)根据题意得:原式=
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2012 |
| 2011 |
| 2011 |
| 2012 |
| 2013 |
| 2012 |
| 1 |
| 2 |
| 2013 |
| 2012 |
| 2013 |
| 4024 |
故答案为:(1)
| 9 |
| 10 |
| 11 |
| 10 |
| 99 |
| 100 |
| 101 |
| 100 |
| 2011 |
| 2012 |
| 2013 |
| 2012 |
点评:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
二次函数y=mx2-3x+2m-4的图象过原点,则m=( )
| A、m=0 | B、m=2 |
| C、m=-2 | D、m=0且m=2 |
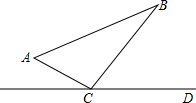 如图,△ABC中,∠ACB=90°,AC=6BC=8.点P从点出发沿A-C-B路径向终点运动,终点为B点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,一点到相应的终点停止运动,某时刻,分别过P和Q作PE⊥L于E,QF⊥L于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.
如图,△ABC中,∠ACB=90°,AC=6BC=8.点P从点出发沿A-C-B路径向终点运动,终点为B点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,一点到相应的终点停止运动,某时刻,分别过P和Q作PE⊥L于E,QF⊥L于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.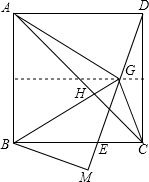 在正方形ABCD中,点E为BC边上的一点,连接DE,点G为DE中点,连接GA、GB、GC,GB与AC交于点H,过点B作BM⊥DE延长线于点M.求证:GA=GB.
在正方形ABCD中,点E为BC边上的一点,连接DE,点G为DE中点,连接GA、GB、GC,GB与AC交于点H,过点B作BM⊥DE延长线于点M.求证:GA=GB.